题目内容
5.(1)计算:($\sqrt{\frac{9}{2}}-\sqrt{\frac{2}{3}}+\sqrt{\frac{3}{2}}$)$÷\sqrt{6}$;(2)解方程:$\frac{2x}{2x-5}$-$\frac{2}{2x+5}$=1.
分析 (1)先根据二次根式的除法法则得到原式=$\sqrt{\frac{9}{2}×\frac{1}{6}}$-$\sqrt{\frac{2}{3}×\frac{1}{6}}$+$\sqrt{\frac{3}{2}×\frac{1}{6}}$,然后把各二次根式化简后合并即可;
(2)先把分式方程化为整式方程,解整式方程,然后进行检验即可得到原方程的解.
解答 解:(1)原式=$\sqrt{\frac{9}{2}×\frac{1}{6}}$-$\sqrt{\frac{2}{3}×\frac{1}{6}}$+$\sqrt{\frac{3}{2}×\frac{1}{6}}$
=$\frac{\sqrt{3}}{2}$-$\frac{1}{3}$+$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$+$\frac{1}{6}$;
(2)去分母得2x(2x+5)-2(2x-5)=(2x-5)(2x+5),
解得x=$\frac{35}{6}$,
经检验,x=$\frac{35}{6}$是原方程的解.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了解分式方程.

练习册系列答案
相关题目
9.若(x-2z)2+|2x-1|+|y+3|=0,则满足等式的x、y、z分别是( )
| A. | x=$\frac{1}{2}$,y=3,z=1 | B. | x=-$\frac{1}{2}$,y=-3,z=-1 | C. | x=$\frac{1}{2}$,y=-3,z=$\frac{1}{4}$ | D. | x=$\frac{1}{2}$,y=3,z=2 |
 列方程解应用题:如图,在长为32m,宽为20m的矩形地面上,修筑同样宽的两条平行且与另一条相互垂直的道路,余下的六个空白的部分作为耕地,要使得耕地的面积为504m2,道路的宽应为多少?
列方程解应用题:如图,在长为32m,宽为20m的矩形地面上,修筑同样宽的两条平行且与另一条相互垂直的道路,余下的六个空白的部分作为耕地,要使得耕地的面积为504m2,道路的宽应为多少?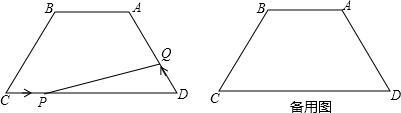
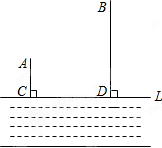 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米.
如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,已知AC=200米,BD=600米,且CD=600米. 如图,已知∠1=∠2,且AB•ED=AD•BC,则△ABC与△ADE相似吗?是说明理由.
如图,已知∠1=∠2,且AB•ED=AD•BC,则△ABC与△ADE相似吗?是说明理由.