题目内容
已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照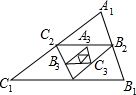 此下去可得第2004个三角形,则第2004个三角形的面积是
此下去可得第2004个三角形,则第2004个三角形的面积是分析:这是一道利用相似三角形的面积比是相似比的平方进行变化的规律题,而任意两个相邻的三角形的面积比为4:1的规律进行变化的,从变化中寻找规律就可以了.
解答:解:∵△A1B1C1∽△A2B2C2∽△A3B3C3 且相似比为2:1,
∴它们面积比为4:1,
∵S△A1B1C1=1=(
)2×0,
S△A2B2C2=
=(
)2×1,
S△A3B3C3=
=(
)2×2,
∴S△AnBnCn=(
)2×(n-1),
∴S△A2004B2004C2004=(
)4006,
故答案为:(
)4006.
∴它们面积比为4:1,
∵S△A1B1C1=1=(
| 1 |
| 2 |
S△A2B2C2=
| 1 |
| 4 |
| 1 |
| 2 |
S△A3B3C3=
| 1 |
| 16 |
| 1 |
| 2 |
∴S△AnBnCn=(
| 1 |
| 2 |
∴S△A2004B2004C2004=(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查了相似三角形的判定及性质,三角形中位线的运用.关键是寻找变化规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
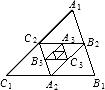 如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是
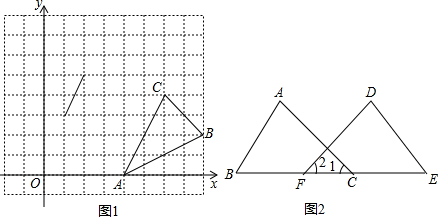
如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是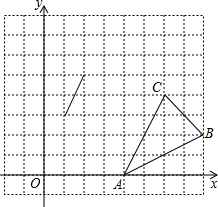 (2012•威海)如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为
(2012•威海)如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为