题目内容
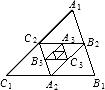 如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是
如图,已知△A1B1C1的面积为1,连接△A1B1C1三边中点得到第二个△A2B2C2,再顺次连接△A2B2C2三边中点得△A3B3C3,照此下去可得第2009个三角形,则第2009个三角形的面积是分析:由A2,B2,C2分别是△A1B1C1各边的中点,根据三角形中位线的性质和有三组对应边的比相等的两个三角形相似得到△A2B2C2∽△A1B1C1,所以S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,得到即S△A2B2C2,=
,
同理可得S△A3B3C3=
×
=(
)2,即可得到第2009个三角形的面积.
| 1 |
| 4 |
同理可得S△A3B3C3=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:∵A2,B2,C2分别是△A1B1C1各边的中点,
∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=
,
∴S△A3B3C3=
×
=(
)2,
∴第2009个三角形的面积是(
)2008.
故答案为:(
)2008.
∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=
| 1 |
| 4 |
∴S△A3B3C3=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴第2009个三角形的面积是(
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题考查了三角形相似的判定与性质:有三组对应边的比相等的两个三角形相似;相似三角形面积的比等于相似比的平方.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn=
如图,已知矩形ABCD的面积为1.A1、B1、C1、D1分别为AB、BC、CD、DA的中点,若四边形A1B1C1D1的面积为S1,A2、B2、C2、D2分别为A1B1、B1C1、C1D1、D1A1的中点,四边形A2B2C2D2的面积记为S2,…,依此类推,第n个四边形AnBnCnDn的面积记为Sn,则Sn= 如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于( )
如图,已知∠A=∠B,AA1,PP1,BB1均垂直于A1B1,AA1=17,PP1=16,BB1=20,A1B1=12,则AP+PB等于( ) 如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=( )
如图,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连接A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2…按此规律继续下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn则θ10=( )
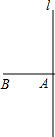 如图,已知直线l,点A在I上,线段AB=1cm,且AB⊥l.我们规定:把线段AB先沿直线l翻折得到A1′B1′(即线段AB与线段A1′B1′关于l成轴对称),再沿射线A1′B1′方向平移1cm得到线段A1B1,称为第一次变换;再将线段A1B1先沿直线l翻折得到A2′B2′,再沿射线A2′B2′方向平移1cm得到线段A2B2.称为第二次变换.
如图,已知直线l,点A在I上,线段AB=1cm,且AB⊥l.我们规定:把线段AB先沿直线l翻折得到A1′B1′(即线段AB与线段A1′B1′关于l成轴对称),再沿射线A1′B1′方向平移1cm得到线段A1B1,称为第一次变换;再将线段A1B1先沿直线l翻折得到A2′B2′,再沿射线A2′B2′方向平移1cm得到线段A2B2.称为第二次变换.