题目内容
 如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD
如图,AB、CD是⊙O的直径,OE⊥AB,OF⊥CD,则∠EOD |
| AC |
 |
| BD |
考点:圆心角、弧、弦的关系
专题:
分析:先由垂直的定义得出∠BOE=∠DOF,再根据同角的余角相等得出∠EOD=∠BOF;由∠AOC=∠BOD,根据在同圆和等圆中,相等的圆心角所对的弧相等得出
=
;由∠BOF=∠DOE,根据在同圆和等圆中,相等的圆心角所对的弦相等得出BF=DE.
 |
| AC |
 |
| BD |
解答:解:∵OE⊥AB,OF⊥CD,
∴∠BOE=∠DOF,
∴∠EOD=∠BOF;
∵∠AOC=∠BOD,
∴
=
;
∵∠BOF=∠DOE,
∴BF=DE.
故答案为:=;=;=.
∴∠BOE=∠DOF,
∴∠EOD=∠BOF;
∵∠AOC=∠BOD,
∴
 |
| AC |
 |
| BD |
∵∠BOF=∠DOE,
∴BF=DE.
故答案为:=;=;=.
点评:本题考查了圆心角、弧、弦的关系定理:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.同时考查了垂直的定义,余角的性质.

练习册系列答案
相关题目
已知⊙O的直径是11cm,点O到直线m的距离是6cm,则⊙O与直线m的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |
 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为
如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为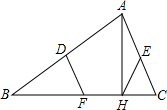 已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH.
已知:如图,D、E、F分别是△ABC三边中点,AH⊥BC于H,求证:DF=EH. 如图,在等腰Rt△ABC中,AB=AC=4
如图,在等腰Rt△ABC中,AB=AC=4 如图,△ABC内接于⊙O,AB=BC,D为⊙O上一点,DB=DC,DB交AC于F.求证:BC=CF.
如图,△ABC内接于⊙O,AB=BC,D为⊙O上一点,DB=DC,DB交AC于F.求证:BC=CF.