题目内容
7. 正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )| A. | (1,2) | B. | (1,-2) | C. | (1,-3) | D. | (1,3) |
分析 过C作CE⊥x轴于E,求出∠BEC=∠BOA=90°,根据正方形的性质得出AB=BC,∠ABC=90°,求出∠BAO=∠CBO,根据全等三角形的判定得出△AOB≌△BEC,根据全等三角形的性质得出OB=CE,AO=BE,即可求出答案.
解答 解:过C作CE⊥x轴于E,则∠BEC=∠BOA=90°,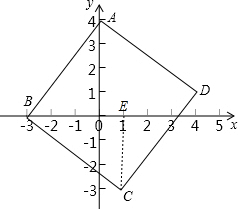
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBO=90°,∠BAO+∠ABO=90°,
∴∠BAO=∠CBO,
在△AOB和△BEC中,
$\left\{\begin{array}{l}{∠BAO=∠CBE}\\{∠AOB=∠BEC}\\{AB=BC}\end{array}\right.$,
∴△AOB≌△BEC(AAS),
∴OB=CE,AO=BE,
∵点A的坐标(0,4),点B的坐标(-3,0),
∴AO=4,OB=3,
∴CE=3,BE=4,
∴OE=4-3=1,
∴C点的坐标为(1,-3),
故选C.
点评 本题考查了点的坐标与图形性质,正方形的性质,全等三角形的性质和判定的应用,能构造直角三角形并求出△AOB≌△BEC是解此题的关键.

练习册系列答案
相关题目
15.下列运算中,结果是a6的是( )
| A. | a2•a3 | B. | a12•a2 | C. | (-a)6 | D. | (a3)3 |
16.下列说法错误的是( )
| A. | 无理数是无限小数 | |
| B. | 如果两条直线被第三条直线所截,那么内错角相等 | |
| C. | 经过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 联结直线外一点与直线上各点的所有线段中,垂线段最短 |
 (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20 ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
 如图,在?ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,∠F=62°,求∠D的度数.
如图,在?ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,∠F=62°,求∠D的度数.