题目内容
12. 如图,在?ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,∠F=62°,求∠D的度数.
如图,在?ABCD中,E是BC上的一点,且AB=BE,AE、DC的延长线相交于点F,∠F=62°,求∠D的度数.
分析 由平行四边形的性质得出∠D=∠B,AB∥CD,得出∠BAE=∠F=62°,由等腰三角形的性质和三角形内角和定理求出∠B=56°,即可得出结果.
解答 解:∵四边形ABCD是平行四边形,
∴∠D=∠B,AB∥CD,
∴∠BAE=∠F=62°,
∵AB=BE,
∴∠AEB=∠BAE=62°,
∴∠B=180°-2×62°=56°,
∴∠D=56°.
点评 本题考查了平行四边形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握平行四边形的性质,由等腰三角形的性质和三角形内角和定理求出∠B是解决问题的关键.

练习册系列答案
相关题目
7. 正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
 正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )| A. | (1,2) | B. | (1,-2) | C. | (1,-3) | D. | (1,3) |
1.如果一个角的补角是130°,那么这个角的余角的度数是( )
| A. | 30° | B. | 40° | C. | 50° | D. | 90° |
2.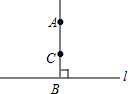 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |