题目内容
17.已知$\frac{1}{x}$-$\frac{1}{y}$=3,则代数式$\frac{2x-8xy-2y}{x-2xy-y}$的值为$\frac{14}{5}$.分析 由条件得出x-y=-3xy,利用整体代入的思想解决问题.
解答 解:∵$\frac{1}{x}$-$\frac{1}{y}$=3,
∴y-x=3xy,x-y=-3xy,
∴$\frac{2x-8xy-2y}{x-2xy-y}$=$\frac{2(x-y)-8xy}{(x-y)-2xy}$=$\frac{-14xy}{-5xy}$=$\frac{14}{5}$.
故答案为$\frac{14}{5}$.
点评 本题考查分式化简求值,解题的关键是学会利用整体代入的思想,学会转化的思想,属于中考常考题型.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
7. 正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
 正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )
正方形ABCD在平面直角坐标系中的位置如图所示,已知点A的坐标(0,4),点B的坐标(-3,0),则点C的坐标是( )| A. | (1,2) | B. | (1,-2) | C. | (1,-3) | D. | (1,3) |
8. 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )
 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
5.方程$\frac{2}{x}=\frac{3}{x-1}$的解为( )
| A. | x=-2 | B. | x=2 | C. | x=-1 | D. | x=$\frac{1}{2}$ |
12.若x,y都是实数,且$\sqrt{2x-1}$+$\sqrt{2-4x}$+y=4,则xy的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不能确定 |
2.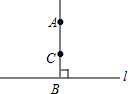 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
 如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
如图所示,因为AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点能作一条垂线 | |
| D. | 垂线段最短 |