题目内容
18.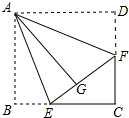 如图正方形ABCD的边长为4,点E、F分别在BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1.
如图正方形ABCD的边长为4,点E、F分别在BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1.(1)求EF的长;
(2)△AEF的面积.
分析 (1)根据勾股定理求出FG,计算即可;
(2)根据翻转变换的性质得到AG=AB=4,∠AGE=∠B=90°,根据三角形的面积公式计算即可.
解答 解:(1)设DF=x,则FG=x,FC=3-x,
由勾股定理得得,(x+1)2=32+(4-x)2,
解得,x=2.4,即FG=DF=2.4,
∴EF=EG+FG=3.4;
(2)由翻转变换的性质可知,AG=AB=4,∠AGE=∠B=90°,
∴△AEF的面积=$\frac{1}{2}$×EFA×AG=6.8.
点评 本题考查的是翻转变换的性质、正方形的性质,翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
8.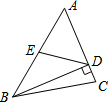 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
 如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )
如图,在△ABC中,BD⊥AC于点D,点E为AB的中点,AD=6,DE=5,则线段BD的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
 如图,将△ABC沿BC方向向右平移得到△DEF,其中BF=10,EC=4,则平移的距离为3.
如图,将△ABC沿BC方向向右平移得到△DEF,其中BF=10,EC=4,则平移的距离为3.