题目内容
解关于x的方程。
m2x+1=m(x+1) (m≠0且m≠1)
m2x+1=m(x+1) (m≠0且m≠1)
解:m2x+1=mx+m
(m2-m)x=m-1,m(m-1)x=m-1
∵m≠0且m≠1,
∴m≠0,m-1≠0
x=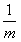
(m2-m)x=m-1,m(m-1)x=m-1
∵m≠0且m≠1,
∴m≠0,m-1≠0
x=
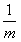

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
用配方法解关于x的方程x2+mx+n=0,此方程可变形为( )
A、(x+
| ||||
B、(x+
| ||||
C、(x+
| ||||
D、(x+
|