题目内容
8.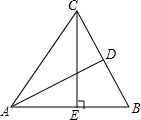 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°,∠BCE=30°,求∠ADB的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°,∠BCE=30°,求∠ADB的度数.
分析 根据AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,可得∠BAD和∠CAD相等,都为30°,∠CEA=90°,从而求得∠ACE的度数,又因为∠BCE=40°,∠ADB=∠BDE+∠ACE+∠CAD,从而求得∠ADB的度数.
解答 解:∵AD是△ABC的角平分线,CE是△ABC的高,∠BAC=50°.
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=25°,∠CEA=90°.
∵∠CEA+∠BAC+∠ACE=180°.
∴∠ACE=40°.
∵∠ADB=∠BCE+∠ACE+∠CAD,∠BCE=30°.
∴∠ADB=40°+30°+35°=95°.
点评 本题考查三角形的内角和、角的平分线、三角形的一个外角等于和它不相邻的内角的和,关键是根据具体目中的信息,灵活变化,求出相应的问题的答案

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
18.对于单项式ab2c4,下列说法中,正确的是( )
| A. | 系数是a,次数是6 | B. | 没有系数,次数是7 | ||
| C. | 系数是1,次数是6 | D. | 系数是1,次数是7 |
13.下列说法正确的是( )
| A. | a一定是正数,-a一定是负数 | B. | -1是最大的负整数 | ||
| C. | 0既没有倒数也没有相反数 | D. | 若a≠b,则a2≠b2 |
20.下列四个“QQ表情”图片中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.若a=b,那么下列各式不一定成立的是( )
| A. | $a-\frac{1}{3}=b-\frac{1}{3}$ | B. | $-\frac{3}{4}a=-\frac{3}{4}b$ | C. | 3a-1=3b-1 | D. | $\frac{a}{c}=\frac{b}{c}$ |