题目内容
16.?ABCD的周长为26cm,相邻两条边长的差为3cm.如果设较长的边为x cm,较短的边为y cm,那么可得方程组为$\left\{\begin{array}{l}{x+y=\frac{26}{2}}\\{x-y=3}\end{array}\right.$.分析 由?ABCD的周长为26cm,根据平行四边形的对边相等,可得两邻边长的和是13cm,又由两邻边长的差是3cm,由此联立方程组即可求得答案.
解答 解:设较长的边为xcm,较短的边为ycm,由题意得
$\left\{\begin{array}{l}{x+y=\frac{26}{2}}\\{x-y=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x+y=\frac{26}{2}}\\{x-y=3}\end{array}\right.$.
点评 此题考查从实际问题中抽象出二元一次方程组,掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
8.当a>b时,能推出$\frac{1}{a}$>$\frac{1}{b}$,则a,b应满足条件( )
| A. | a>0,b>0 | B. | a<0,b<0 | C. | a>0,b<0 | D. | 以上答案都不对 |
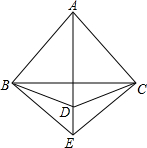 如图,AB=AC,AD平分∠BAC,求证:∠DBE=∠DCE.
如图,AB=AC,AD平分∠BAC,求证:∠DBE=∠DCE. 如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.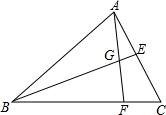 如图所示,在△ABC中,BF:FC=3:1,G为AF的中点,连接BG并延长交AC于点E,则BG:BE=$\frac{7}{8}$.
如图所示,在△ABC中,BF:FC=3:1,G为AF的中点,连接BG并延长交AC于点E,则BG:BE=$\frac{7}{8}$.