题目内容
12.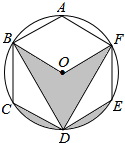 如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为3π(结果保留π).
如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为3,则阴影部分的面积为3π(结果保留π).
分析 首先连接OC,OE,分别交BD,DF于点M,N,易证得S△OBM=S△DCM,同理:S△OFN=S△DEN,则可得S阴影=S扇形OCE.
解答 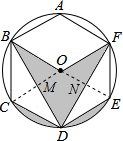 解:连接OC,OE,分别交BD,DF于点M,N,
解:连接OC,OE,分别交BD,DF于点M,N,
∵正六边形ABCDEF内接于⊙O,
∴∠BOC=60°,∠BCD=∠COE=120°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠OCD=∠OCB,
∵BC=CD,
∴∠CBD=∠CDM=30°,BM=DM,
∴∠OBM=30°,S△DCM=S△BCM,
∴∠OBM=∠CBD,
∴OM=CM,
∴S△OBM=S△BCM,
∴S△OBM=S△DCM,
同理:S△OFN=S△DEN,
∴S阴影=S扇形OCE=$\frac{120×π×{3}^{2}}{360}$=3π.
故答案为:3π.
点评 此题考查了正多边形与圆的知识以及扇形的面积公式.注意证得S阴影=S扇形OCE是关键.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | a6÷a3=a2 | B. | 3a2•2a=6a3 | C. | (3a)2=3a2 | D. | (a+b)2=a2+b2 |
7.不等式3x+10≤1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列运算中,正确的是( )
| A. | x2•x3=x5 | B. | (x3)2=x5 | C. | 3x2-x2=3 | D. | (2x)2=2x2 |
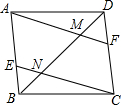 如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.
如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.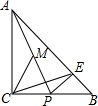 如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点.
如图,△ACB为等腰直角三角形,△PBE也为等腰直角三角形,M为AP的中点. 如图,直线a、b被直线c、d所截.若∠1=∠2,∠3=125°,则∠4的大小为55°.
如图,直线a、b被直线c、d所截.若∠1=∠2,∠3=125°,则∠4的大小为55°.