Question

【题目】学习与探究：

在等边△ABC中，P是射线AB上的一点．

（1）探索实践：

如图1，P是边AB的中点，D是线段CP上的一个动点，以CD为边向右侧作等边△CDE，DE与BC交于点M，连结BE．

①求证：AD＝BE；

②连结BD，当DB+DM最小时，试在图2中确定D的位置，并说明理由；（要求用尺规作图，保留作图痕迹）

③在②的条件下，求△CME与△ACM的面积之比．

（2）思维拓展：

如图3，点P在边AB的延长线上，连接CP，点B关于直线CP的对称点为B'，连结AB'，CB'，AB'交BC于点N，交直线CP于点G，连结BG．请判断∠AGC与∠AGB的大小关系，并证明你的结论．

Answer 1

【答案】（1）①见解析，②见解析，③1:3；（2）∠AGC＝∠AGB，理由见解析

【解析】

1）探索实践

①根据等边三角形的性质可得AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°，可得∠ACD＝∠BCE，根据“SAS”可证△ACD≌△BCE，即可得AD＝BE；

②根据等腰三角形的性质可得AD＝BD，即BD+DM＝AD+DM，则当点A，点D，点M三点共线且AM⊥BC时，BD+DM值最小，即AM平分∠CAB；

③根据等边三角形的性质可求AM＝3ME，由△CME与△ACM是等高的两个三角形，即△CME与△ACM的面积之比等于ME与AM的比值；

（2）思维拓展

根据轴对称的性质和等腰三角形的性质可得∠CAB'＝∠CBG，可证点A，点B，点G，点C四点共圆，可得∠AGC＝∠ABC＝60°，∠AGB＝∠ACB＝60°，即∠AGC＝∠AGB．

（1）探索实践

①在等边△ABC与等边△CDE中：AC＝BC，CE＝CD，∠ACB＝∠DCE＝60°，

∴∠ACD+∠DCM＝∠DCM+∠BCE，

∴∠ACD＝∠BCE

∴△ACD≌△BCE（SAS）

∴AD＝BE

（2）②如图，作∠BAC的平分线交CP于D，连结BD，

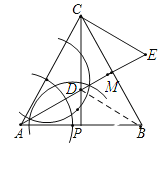
∵P是边等边△ABC中AB边的中点

∴CP是AB边上的中线，

由“等腰三角形的三线合一”性质知，CP是AB的垂直平分线，CP平分∠ACB，

∴DB＝DA，∠PCB＝30°

要使DB+DM最小，只要DA+DM最小，即当A，D，M共线时，且AM⊥BC时，AM最小，

此时DB+DM最小

③∵∠ACD＝∠CAD＝∠DCM＝∠ECM＝30°，CM⊥AM

∴DC＝DA＝DE，DM＝EM＝DE，

∴AM＝3ME

又∵Rt△CME的边ME上的高与Rt△ACM的边AM上的高均是CM

∴S△CME：S△ACM＝1：3

（2）思维拓展

∠AGC＝∠AGB

理由如下：∵点B关于直线CP的对称点为B'，

∴BC＝CB'，∠CB'G＝∠CBG，

∴AC＝BC＝B'C

∴∠CAB'＝∠CB'A，

∴∠CAB'＝∠CBG，

∴点A，点B，点G，点C四点共圆，

∴∠AGC＝∠ABC＝60°，∠AGB＝∠ACB＝60°，

∴∠AGC＝∠AGB