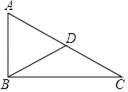
题目内容
【题目】某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为_____m(结果保留一位小数,参考数据:sin53°≈![]() , cos53°≈
, cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).

【答案】1.2.
【解析】
过点D作DO⊥AH于点O,先证明△ABC∽△AOD得出![]() =
=![]() ,再根据已知条件求出AO,则OH=AH-AO=DG.
,再根据已知条件求出AO,则OH=AH-AO=DG.
过点D作DO⊥AH于点O,如图:

由题意得CB∥DO,
∴△ABC∽△AOD,
∴![]() =
=![]() ,
,
∵∠CAB=53°,tan53°=![]() ,
,
∴tan∠CAB=![]() =
=![]() ,
,
∵AB=1.74m,
∴CB=2.32m,
∵四边形DGHO为长方形,
∴DO=GH=3.05m,OH=DG,
∴![]() =
=![]() ,
,
则AO=2.2875m,
∵BH=AB=1.75m,
∴AH=3.5m,
则OH=AH-AO≈1.2m,
∴DG≈1.2m.
故答案为1.2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目