题目内容
 如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD•DC=PA•BC.
如图,ABCD是⊙O的内接四边形,DP∥AC,交BA的延长线于P,求证:AD•DC=PA•BC.
 证明:如图,连接AC,连接BD.
证明:如图,连接AC,连接BD.∵DP∥AC,
∴∠PDA=∠DAC.
∵∠DAC=∠DBC,
∴∠PDA=∠DBC.
∵四边形ABCD是圆内接四边形,
∴∠DAP=∠DCB.
∴△PAD∽△DCB.
得PA:DC=AD:BC,
即AD•DC=PA•BC.
分析:要证AD•DC=PA•BC,需证△PAD∽△DCB;由DP∥AC,可得∠ADP=∠DAC=∠DBC;由于∠DAP是圆内接四边形ABCD的一个外角,故有∠DAP=∠DCB;从而△PAD∽△DCB成立,由此得证.
点评:本题考查了平行线的性质,圆周角定理,相似三角形的判定和性质等知识.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=
如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若再增加一个条件,就可使四边形ABCD成为等腰梯形,你所增加的条件是(只写出一个条件,图中不再增加其他的字母和线段.(给出证明)
如图四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若再增加一个条件,就可使四边形ABCD成为等腰梯形,你所增加的条件是(只写出一个条件,图中不再增加其他的字母和线段.(给出证明)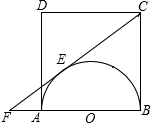 如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.
如图,ABCD是边长为2 a的正方形,AB为半圆O的直径,CE切⊙O于E,与BA的延长线交于F,求EF的长.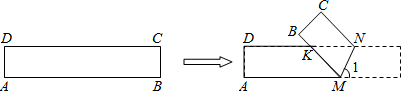
 如图,ABCD是正方形,G是BC上的一点,DE⊥AG于E,BF⊥AG于F.
如图,ABCD是正方形,G是BC上的一点,DE⊥AG于E,BF⊥AG于F.