题目内容
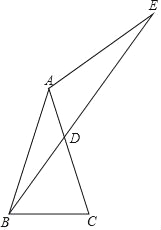
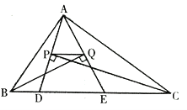
【题目】如图，在△ABC 中，AB＝AD，CB＝CE．
（1）当∠ABC＝90°时（如图①），∠EBD＝ °；
（2）当∠ABC＝n°（n≠90）时（如图②），求∠EBD 的度数（用含 n 的式子表示）．
【答案】(1)45;(2) ∠DBE=90°-
n°．
【解析】
（1）根据等腰三角形的性质，即可得到∠ABD=∠ADB=（180°-∠A），∠CBE=∠CEB=（180°-∠C），再根据三角形内角和定理，即可得到∠DBE的度数；
（2）运用（1）中的方法进行计算，即可得到∠EBD的度数．
解：（1）∵AB=AD，CB=CE，
∴∠ABD=∠ADB=（180°-∠A），∠CBE=∠CEB=（180°-∠C），
∵∠ABC=90°，
∴∠A+∠C=90°，
∴△BDE中，∠DBE=180°-（∠ADB+∠CEB）
=180°-（180°-∠A）-（180°-∠C）
=（∠A+∠C）
=×90°
=45°，
故答案为：45．
（2）∵AB=AD，CB=CE，
∴∠ABD=∠ADB=（180°-∠A），∠CBE=∠CEB=（180°-∠C），
∵∠ABC=n°，
∴∠A+∠C=180°-n°，
∴△BDE中，∠DBE=180°-（∠ADB+∠CEB）
=180°-（180°-∠A）-（180°-∠C）
=（∠A+∠C）=×（180°-n°）
=90°-n°．
阅读快车系列答案
【题目】某工地因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如表：
租金（单位：元/台时） | 挖掘土石方量（单位：m3/台时） | |
甲型机 | 100 | 60 |
乙型机 | 120 | 80 |
（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型的挖掘机各需多少台？
（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有几种不同的租用方案．
