题目内容
12.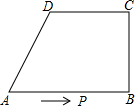 在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,以每秒1个单位的速度沿A→B→C→D运动.若设点P运动的时间为x秒,△APC的面积为S.则当x等于多少时,△APC的面积S=4.5?(如答案有多样,可根据需要,自行画图,并解答.)
在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,以每秒1个单位的速度沿A→B→C→D运动.若设点P运动的时间为x秒,△APC的面积为S.则当x等于多少时,△APC的面积S=4.5?(如答案有多样,可根据需要,自行画图,并解答.)
分析 需要分类讨论:当点P在AB边上,点P在BC边上,点P在CD边上,根据三角形的面积公式求解可得.
解答 解: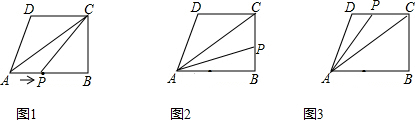
①如图1,当点P在AB边上时,S△APC=$\frac{1}{2}$AP•BC=$\frac{1}{2}$•x×3=4.5,
解得x=3,即当x=3时,△APC的面积S=4.5;
②如图2,当点P在BC边上时,S△APC=$\frac{1}{2}$PC•AB=$\frac{1}{2}$•(7-x)×4=4.5,
解得x=$\frac{19}{4}$,即当x=$\frac{19}{4}$时,△APC的面积S=4.5;
③如图,当点P在CD边上时,S△APC=$\frac{1}{2}$PC•BC=$\frac{1}{2}$•(x-7)×3=4.5,
解得x=10,即当x=10时,△APC的面积S=4.5;
综上所述,当x的值为3,$\frac{19}{4}$,10时,△APC的面积S=4.5.
点评 本题考查了动点函数图象.对于动点问题,需要分类讨论,以防漏解或错解.

练习册系列答案
相关题目
15.若∠α与∠β的两边分别平行,且∠α=(x-10)°,∠β=(2x+25)°,则∠α的度数为( )
| A. | 45° | B. | 55° | C. | 45°或55° | D. | 55°或65° |
20.比较355,444,533的大小,正确的是( )
| A. | 444>355>533 | B. | 533>444>355 | C. | 355>444>533 | D. | 355>533>444 |
4.下列等式由左边到右的变形中,属于因式分解的是( )
| A. | mx+nx+k=(m+n)x+k | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)-3x | D. | (a+b)(a-b)=a2-b2 |
1.在早餐店里,王伯伯买5个馒头,3个包子,老板少拿2元,只要50元.李太太买了11个馒头,5个包子,老板以售价的九折优待,只要90元.若馒头每个x元,包子每个y元,则下列可表示题目中的数量关系的二元一次方程组为( )
| A. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90×0.9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90÷0.9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90×0.9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90÷0.9}\end{array}\right.$ |
 如图,点C、D在线段AB上,△PCD是等边三角形,若∠APB=120°,求证:△ACP∽△PDB.
如图,点C、D在线段AB上,△PCD是等边三角形,若∠APB=120°,求证:△ACP∽△PDB.