题目内容
1.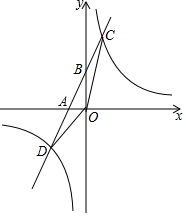 如图,在平面直角坐标系中,一次函数y=ax+2(a≠0)的图象分别与x轴、y轴交于点A,B,与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于C(1,m),D(n,-2)两点,连接OD,OC,其中tan∠BAO=2.
如图,在平面直角坐标系中,一次函数y=ax+2(a≠0)的图象分别与x轴、y轴交于点A,B,与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于C(1,m),D(n,-2)两点,连接OD,OC,其中tan∠BAO=2.(1)求一次函数的表达式;
(2)求反比例函数的表达式和△COD的面积.
分析 (1)由一次函数图象上点的坐标特征可得出点B的坐标,结合tan∠BAO=2可得出OA的长度,进而得出点A的坐标,根据点A、B的坐标利用待定系数法,即可求出一次函数的表达式;
(2)由一次函数图象上点的坐标特征可得出点C、D的坐标,根据点C的坐标利用待定系数法,即可求出反比例函数的表达式,再根据三角形的面积公式即可求出△COD的面积.
解答 解:(1)当x=0时,y=ax+2=2,
∴点B(0,2).
∵tan∠BAO=$\frac{BO}{AO}$=2,
∴AO=1,
∴点A(-1,0).
将点A(-1,0)代入y=ax+2中,
0=-a+2,解得:a=2,
∴一次函数的表达式为y=2x+2.
(2)∵点C(1,m)、D(n,-2)在y=2x+2的函数图象上,
∴m=4,n=-2,
∴C(1,4),D(-2,-2).
将点C(1,4)代入y=$\frac{k}{x}$中,
4=$\frac{k}{1}$,解得:k=4,
∴反比例函数的表达式为y=$\frac{4}{x}$.
S△COD=$\frac{1}{2}$OA•(yC-yD)=$\frac{1}{2}$×1×[4-(-2)]=3.
点评 本题考查了反比例函数与一次函数的交点问题、解直角三角形、待定系数法求一次(反比例)函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)通过解直角三角形求出点A的坐标;(2)根据点的坐标利用待定系数法求出函数关系式.

练习册系列答案
相关题目
16.下列各式能用平方差公式计算的是( )
| A. | (3a+b)(a-b) | B. | (3a+b)(-3a-b) | C. | (-3a-b)(-3a+b) | D. | (-3a+b)(3a-b) |
13.下列图形中,∠2>∠1的是( )
| A. | 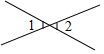 | B. |  | C. | 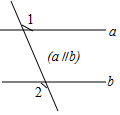 | D. |  |
10.下列各式成立的是( )
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{{6}^{2}}$=±6 | D. | $\sqrt{(-5)^{2}}$=±5 |
 如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.
如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.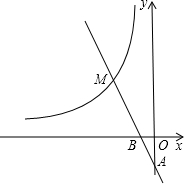 如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).
如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).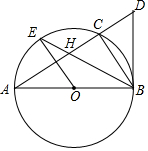 如图,AB是⊙O的直径,C是⊙O是一点,过点B作⊙O的切线,与AC延长线交于点D,连接BC,OE∥BC交⊙O于点E,连接BE交AC于点H.
如图,AB是⊙O的直径,C是⊙O是一点,过点B作⊙O的切线,与AC延长线交于点D,连接BC,OE∥BC交⊙O于点E,连接BE交AC于点H.