题目内容
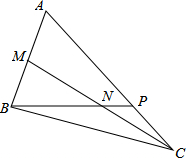 已知:M是AB的中点,AP=2PC,BP=4,求PN的长.
已知:M是AB的中点,AP=2PC,BP=4,求PN的长.考点:三角形中位线定理
专题:
分析:过点M作MD∥PB,交AC于点D,根据三角形的中位线定理可得出MD=2,从而得出NP=1.
解答: 解:过点M作MD∥PB,交AC于点D,
解:过点M作MD∥PB,交AC于点D,
∵M是AB的中点,
∴MD=
PB,
∵BP=4,
∴MD=2,
∵AP=2PC,
∴点P为CD中点,
∴PN=
MD,
∴NP=1.
 解:过点M作MD∥PB,交AC于点D,
解:过点M作MD∥PB,交AC于点D,∵M是AB的中点,
∴MD=
| 1 |
| 2 |
∵BP=4,
∴MD=2,
∵AP=2PC,
∴点P为CD中点,
∴PN=
| 1 |
| 2 |
∴NP=1.
点评:本题考查了三角形的中位线定理,以及逆定理,解此题的关键是利用点M为AB的中点,作出三角形ABP的中位线.

练习册系列答案
相关题目
 如图,∠ACB=∠BDC=90°,BD=4,BC=5,则AC=
如图,∠ACB=∠BDC=90°,BD=4,BC=5,则AC=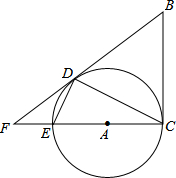 在Rt△ABC中,∠C=90°,BC=6,AC=3,过点B作以点A为圆心,AC为半径的⊙A的切线,切点为D,延长CA交圆于点E,交切线BD的延长线于点F,连接DE.
在Rt△ABC中,∠C=90°,BC=6,AC=3,过点B作以点A为圆心,AC为半径的⊙A的切线,切点为D,延长CA交圆于点E,交切线BD的延长线于点F,连接DE. 
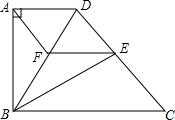 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.