题目内容
 如图,长方形ABCD中,AB=a,BC=b (a,b为正整数,且a>b),中间小长方形离开四周的距离都等于1,且面积是长方形ABCD的一半,则a=
如图,长方形ABCD中,AB=a,BC=b (a,b为正整数,且a>b),中间小长方形离开四周的距离都等于1,且面积是长方形ABCD的一半,则a=考点:面积及等积变换
专题:
分析:首先根据题意可得方程:
ab=(a-2)(b-2),整理此方程,可解得:a=4+
,由a,b为正整数,可得b-4=1或2或4或8,又由a>b,然后分别求解即可求得答案.
| 1 |
| 2 |
| 8 |
| b-4 |
解答:解:根据题意得:
ab=(a-2)(b-2),
即:ab-4a=4b-8,
可得:(b-4)a=4b-8,
解得:a=
=
=4+
,
∵a,b为正整数,
∴b-4=1或2或4或8,
∵a>b,
∴当b-4=1时,a=12,b=5;
当b-4=2时,a=8,b=6;
当b-4=4时,a=6,b=8(舍去);
当b-4=8时,a=5,b=12(舍去);
∴a=12或8.
故答案为:12或8.
| 1 |
| 2 |
即:ab-4a=4b-8,
可得:(b-4)a=4b-8,
解得:a=
| 4b-8 |
| b-4 |
| 4(b-4+2) |
| b-4 |
| 8 |
| b-4 |
∵a,b为正整数,
∴b-4=1或2或4或8,
∵a>b,
∴当b-4=1时,a=12,b=5;
当b-4=2时,a=8,b=6;
当b-4=4时,a=6,b=8(舍去);
当b-4=8时,a=5,b=12(舍去);
∴a=12或8.
故答案为:12或8.
点评:此题考查了矩形的性质与面积与等积变换问题.此题难度较大,解题的关键是根据题意列方程,然后求得a=4+
,再利用分类讨论思想求解即可.
| 8 |
| b-4 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知⊙O1的半径是5cm,⊙O2的半径是2cm,O1O2=3cm,则两圆的位置关系是( )
| A、外离 | B、内切 | C、相交 | D、内含 |
 跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有( )种方法.
跳格游戏如图:人从格外进入格中,每次可向前跳1格或2格,那么人从格外跳到第6格可以有( )种方法.| A、6 | B、8 | C、13 | D、15 |
多边形的边数增加2,这个多边形的内角和增加( )
| A、90° | B、180° |
| C、360° | D、540° |

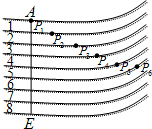 在田径比赛中的标准跑道一般是由长为85.96米的两条直道和半径为36米的两条半圆弧跑道组成.标准跑道分为8道,每条跑道宽1.25米.国际田联规定:
在田径比赛中的标准跑道一般是由长为85.96米的两条直道和半径为36米的两条半圆弧跑道组成.标准跑道分为8道,每条跑道宽1.25米.国际田联规定: 如图,四边形ABCD的对角线AC、BD相交于点O,
如图,四边形ABCD的对角线AC、BD相交于点O, 如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=∠EAB,AE是⊙O的直径吗?为什么?
如图,A、B、E、C四点都在⊙O上,AD是△ABC的高,∠CAD=∠EAB,AE是⊙O的直径吗?为什么?