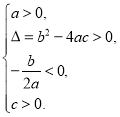题目内容
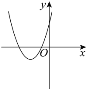
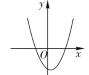
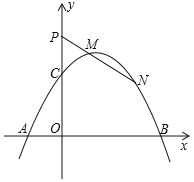
【题目】如图是抛物线![]() 的部分图象,其顶点为
的部分图象,其顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,连接
,连接![]() .以下结论:①
.以下结论:①![]() ;②抛物线经过点
;②抛物线经过点![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() .其中正确的是( )
.其中正确的是( )
A.①③B.②③C.①④D.②④
【答案】D
【解析】
根据抛物线与y轴交于点(0,3),可得出k的值为4,从而得出抛物线的解析式为![]() ,将(-2,3)代入即可判断正确与否,抛物线与x轴的交点A(1,0),因此得出三角形的面积为2,当x-3<x<1时,y>0.据此判断④正确.
,将(-2,3)代入即可判断正确与否,抛物线与x轴的交点A(1,0),因此得出三角形的面积为2,当x-3<x<1时,y>0.据此判断④正确.
解:把(0,3)代入抛物线解析式求出k=4,选项①错误,
由此得出抛物线解析式为:![]() ,
,
将(-2,3)代入解析式可得出选项②正确;
抛物线与x轴的两交点分别为(1,0),(-3,0),
∴OA=1,
∵点M到x轴的距离为4,
∴![]() ,选项③错误;
,选项③错误;
∵当x-3<x<1时,y>0.
∵![]()
∴y>0,选项④正确,
故答案为D.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
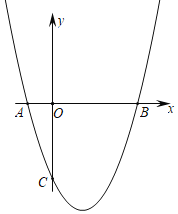
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.