题目内容
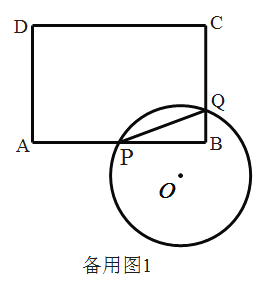
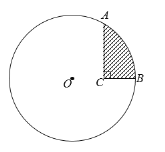
【题目】如图,⊙O的半径为![]() ,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=
,A、B为⊙O上两点,C为⊙O内一点,AC⊥BC,AC=![]() ,BC=
,BC=![]() .
.
(1)判断点O、C、B的位置关系;
(2)求图中阴影部分的面积.
【答案】(1)O、C、B三点在一条直线上,见解析;(2)
【解析】
(1)连接OA、OB、OC,证明∠ABC=∠ABO=60°,从而证得O、C、B三点在一条直线上;
(2)利用扇形面积与三角形面积的差即可求得答案.
(1)答:O、C、B三点在一条直线上.
证明如下:连接OA、OB、OC,

在![]() 中,
中,
![]() ,
,
∵![]()
∴∠ABC=60°,
在![]() 中,
中,
∵OA=OB=AB![]() ,
,
∴△OAB是等边三角形,
∴∠ABO=60°,
故点C在线段OB上,即O、C、B三点在一条直线上.
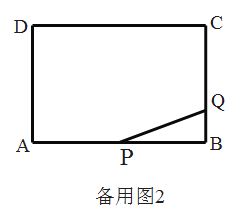
(2)如图,

由(1)得:△OAB是等边三角形,
∴∠O=60°,
![]()
∴![]()
![]()
![]()
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目