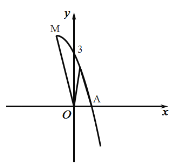题目内容
【题目】如图,已知点![]() 在
在![]() 的直径
的直径![]() 延长线上,点
延长线上,点![]() 为
为![]() 上,过
上,过![]() 作
作![]() ,与
,与![]() 的延长线相交于
的延长线相交于![]() ,
,![]() 为
为![]() 的切线,
的切线,![]() ,
,![]() .
.
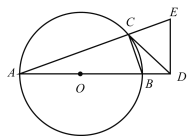
(1)求证:![]() ;
;
(2)求![]() 的长;
的长;
(3)若![]() 的平分线与
的平分线与![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的内心,求
的内心,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用同角的余角相等得出∠E=∠ECD,从而得出结论;
(2)利用直角△OCD和直角△ADE中的勾股定理列出方程解得BD的长;
(3)连接![]() ,
,![]() ,
,![]() ,根据
,根据![]() 平分
平分![]() 求出
求出![]() ,利用同弧所对的圆周角相等得出
,利用同弧所对的圆周角相等得出![]() ,从而得出
,从而得出![]() ,即FP=FB.
,即FP=FB.
解:(1)证明:连接![]() ,
,
∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴由勾股定理可得,![]() ,
,
∵![]() ,
,
∴由勾股定理可得,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去).
(舍去).
(3)连接![]() ,
,![]() ,
,![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为直径,
为直径,![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的内心,
的内心,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


练习册系列答案
相关题目
【题目】4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:
两球所标数字之和 | 3 | 4 | 5 | 6 | 7 |
奖励的购书券金额(元) | 0 | 0 | 30 | 60 | 90 |
(1)通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率;
(2)书城规定:如果顾客不愿意参加摸奖,那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中,你认为哪种方式对顾客更合算?请通过求平均教的方法说明理由.