��Ŀ����
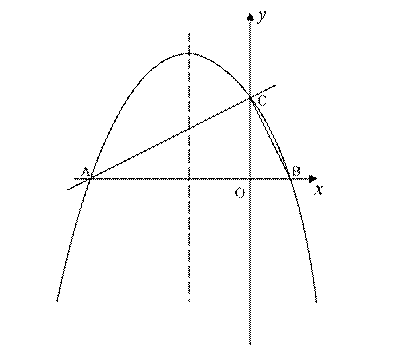
��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��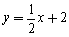 ��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����
��x �ύ�ڵ�A����y�ύ�ڵ�C��������y=ax2+bx+c�ĶԳ�����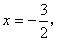 �Ҿ���A��C���㣬��x�����һ����Ϊ��B��
�Ҿ���A��C���㣬��x�����һ����Ϊ��B��
��1����4�֣���ֱ��д����B�����ꣻ���������߽���ʽ��
��2����4�֣�����PΪֱ��AC�Ϸ����������ϵ�һ�㣬����PA��PC�����PAC����������ֵ���������ʱ��P�����꣮
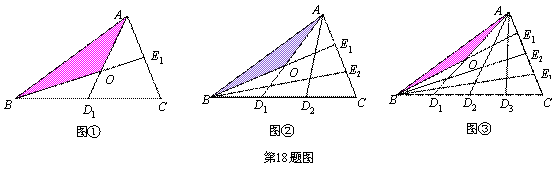
 ��3����4�֣����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3����4�֣����������Ƿ���ڵ�M������M��MN��ֱx���ڵ�N��ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
|

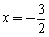
(1) ��B(1,0)
(2)
��y=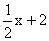 ��x=0ʱ��y��2, ��y=0ʱ��x=��4
��x=0ʱ��y��2, ��y=0ʱ��x=��4
�� C(0,2),A(��4,0) ��������y=ax2+bx+c��A(��4,0), B(1,0)
����������߽���ʽΪy=a(x+4)(x��1)
 �֡������߹���C(0,2) ��2=��4a ��a=
�֡������߹���C(0,2) ��2=��4a ��a=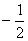
��y=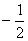 x2
x2 x+2
x+2
(2)��P��m,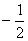 m2
m2 m+2).
m+2).
����P��PQ��x�ύAC�ڵ�Q
��Q(m, m+2)
m+2)
��PQ=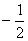 m2
m2 m+2��(
m+2��( m+2)
m+2)
=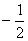 m2��2m
m2��2m
��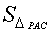 =
=
 PQ
PQ 4
4
 =2PQ=��m2��4m=��(m+2)2+4
=2PQ=��m2��4m=��(m+2)2+4
�൱m=��2ʱ����PAC����������ֵ��4
��ʱP����2��3��
��3����Rt��AOC��tan��CAO= ��Rt��BOC��tan��BCO=
��Rt��BOC��tan��BCO=
���CAO=��BCO �ߡ�BCO+��OBC=90��
���CAO+��OBC=90�� ���ACB=90��
�� ��ABC�צ�ACO�צ�CBO
�� ��M����C���غϣ���M��0��2��ʱ����MAN�צ�BAC
�� ���������ߵĶԳ��ԣ���M(��3,2) ʱ����MAN�צ�ABC
�� ����M�ڵ�������ʱ����M��n,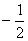 n2
n2 n+2������N(n,0)
n+2������N(n,0)
�� MN= n2+
n2+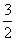 n��2 , AN=n+4
n��2 , AN=n+4
��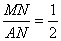 ʱ��MN=
ʱ��MN= AN ��
AN �� n2+
n2+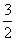 n��2=
n��2= (n+4)
(n+4)
n2+2n��8=0 �� n1= ��4(��), n2=2
��M��2����3��
��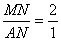 ʱ��MN=2AN
ʱ��MN=2AN  n2+
n2+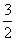 n��2=2(n+4)
n��2=2(n+4)
n2��n��20=0 �� n1= ��4(��), n2=5
��M��5����18��
��������������M1��0��2��,M2(��3,2), M3��2����3��,M4��5����18��, ʹ���Ե�
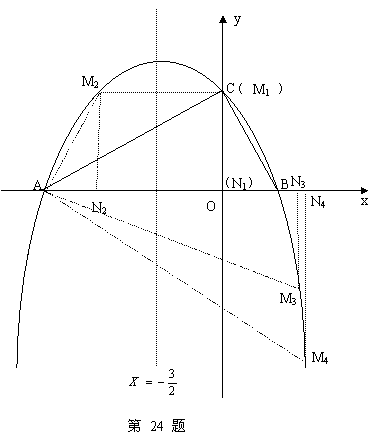 A��M��N��������������ABC����.
A��M��N��������������ABC����.

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д����꼶��1����ѧ������ɿ���ѧϰ�����ʽ��������е����ݷ�����
�����ÿ� ��ʱ������μ�����������ÿλͬѧ������������������Զ�����ܡ�Ǧ����ѡһ�����ѵ����ѵ�������˲��ԣ��ֽ���Ŀѡ�������ѵ��������ʱ����Ͷ�����Գɼ���������������ͳ��ͼ��
��ʱ������μ�����������ÿλͬѧ������������������Զ�����ܡ�Ǧ����ѡһ�����ѵ����ѵ�������˲��ԣ��ֽ���Ŀѡ�������ѵ��������ʱ����Ͷ�����Գɼ���������������ͳ��ͼ��
��Ŀѡ���������ͳ��ͼ ѵ��������ʱ����Ͷ�����Խ�����ͳ��ͼ
 | |||
 | |||
������������ṩ����Ϣ�ش��������⣺
��1����3�֣�����ͼ���������ֵ�����Բ�Ľ�Ϊ  �ȣ��ð��ѧ�� �ˣ�
�ȣ��ð��ѧ�� �ˣ�
ѵ��������ʱ�� ��Ͷ��ƽ��ÿ���˵Ľ������� ��
��Ͷ��ƽ��ÿ���˵Ľ������� ��
��2����5�֣���ʦ������ѡ��Ǧ��ѵ����3��������1��Ů������ѡ����ѧ���Ƚ��в��ԣ������б�������ͼ�ķ�����ǡ��ѡ�����������ĸ��ʣ�
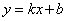 ������һ�����������ޣ���ֱ��
������һ�����������ޣ���ֱ��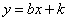 ��������������
��������������
 A B
A B
 C.
C.  D.
D. 
 ����a��b��������������������
����a��b�������������������� .
. ��3 C.3,4,8 D.4,5��6
��3 C.3,4,8 D.4,5��6 ��
��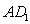 �ཻ�ڵ�O����AOB�������Ϊ
�ཻ�ڵ�O����AOB�������Ϊ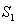 ����ͼ�ڽ���BC��AC�ֱ�3�ȷݣ�
����ͼ�ڽ���BC��AC�ֱ�3�ȷݣ�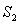 �������� �������ƣ���
�������� �������ƣ���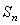 �ɱ�ʾΪ .(�ú�
�ɱ�ʾΪ .(�ú�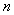 �Ĵ���ʽ��ʾ������
�Ĵ���ʽ��ʾ������