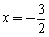题目内容
在平行四边形ABCD中，E为BC边上的一点.连结AE.
（1）若AB=AE, 求证:∠DAE=∠D；
（2）若点E为BC的中点，连接BD，交AE于F,求EF︰FA的值.
1）证明：∵四边形ABCD为平行四边形，
∴ ∠B=∠D AD∥BC.
∴∠AEB=∠EAD. 又∵AE=AB ∴∠B=∠AEB.
∴∠B=∠EAD. ∠EAD=∠D-
（2）∵AD∥BC
∴∠FAD=∠FEB，∠ADF=∠EBF
∴△ADF∽△EBF
EF︰FA= BE︰AD= BE︰ BC=1︰2
练习册系列答案
相关题目
= ．
中，∠C
=90°, ∠A
= CB ．若将边
与边CA重合，其中点
与点C重合．将三角板
角为
，旋转过程中边
．
∥AB；
，当
°= 
，
°= 
，
°=
°= 
°= 
°=
）
的图象在
S△BOC = 1:2，则k的值为（ ）
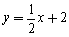与x 轴交于点A，与y轴交于点C．抛物线y=ax2+bx+c的对称轴是
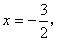且经过A、C两点，与x轴的另一交点为点B．
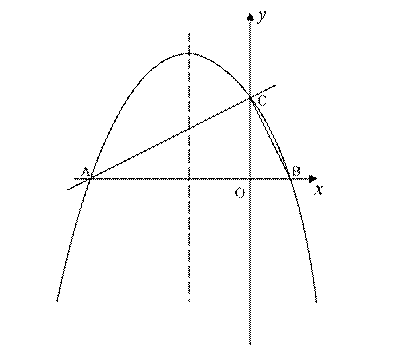（3）（4分）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
