题目内容
12.己知2y与x+2成正比例,且当x=2时,y的值为-6.(1)求y与x之间的函数关系式;
(2)求(1)中所求函数的图象与两坐标轴围成的三角形的周长.
分析 (1)由于2y与x+2成正比例,可设2y=k(x+2)(k≠0),再把(2,-6)代入可计算出k,从而得到y与x之间的函数关系式;
(2)先根据坐标轴上点的坐标特征得到直线与x轴交于点A(-2,0),与y轴交于点B(0,-3),再利用两点间的距离公式计算出AB,然后计算三角形的周长.
解答 解:(1)设2y=k(x+2)(k≠0),
将x=2,y=-6代入得-12=4k,解得k=-3,
所以2y=-3(x+2),
所以y=-1.5x-3;
(2)设y=-1.5x-3与x轴交于点A,与y轴交于点B,则A点坐标为(-2,0),B点坐标为(0,-3),
所以AB=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,
所以△ABC的周长为5+$\sqrt{13}$.
点评 本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
2.下列各式不能因式分解的是( )
| A. | a2-b2 | B. | a2-2a+1 | C. | ab-a | D. | a2+b2 |
3.若分式$\frac{{x}^{2}-9}{x-3}$的值为0,则x的值等于( )
| A. | 0 | B. | ±3 | C. | 3 | D. | -3 |
4.一名射击运动员,射靶10次,射击成绩分别为(单位:环):9,10,8,7,7,8,9,10,9,8,则他射中9环及9环以上的频率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
1.如图:∠1和∠2是同位角的是( )


| A. | ②③ | B. | ①②③ | C. | ①②④ | D. | ①④ |
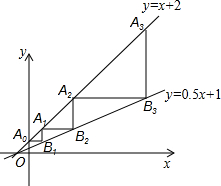 如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.
如图,直线y=x+2与y轴相交于点A0,过点A0作x轴的平行线交直线y=0.5x+1于点B1,过点B1作y轴的平行线交直线y=x+2于点A1,再过点A1作x轴的平行线交直线y=0.5x+1于点B2,过点B2作y轴的平行线交直线y=x+2于点A2,…,依此类推,得到直线y=x+2上的点A1,A2,A3,…,与直线y=0.5x+1上的点B1,B2,B3,…,则An-1Bn的长为2n.