题目内容
4.若方程2x2-x-m=0有有理根,则m的最小正整数值为1.分析 根据根的判别式得出关于m的不等式,求出即可.
解答 解:∵方程2x2-x-m=0有有理根,
∴△=(-1)2-4×2×(-m)≥0,
解得:m≥-$\frac{1}{8}$,
所以m的最小正整数值是1,
故答案为:1.
点评 本题考查了解一元二次方程的根的判别式的应用,能正确理解根的判别式的内容是解此题的关键,注意:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0),当b2-4ac>0时,方程有两个不相等的实数根,当b2-4ac=0时,方程有两个相等的实数根,当b2-4ac<0时,方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
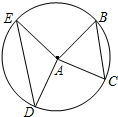 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知BC=6,∠BAC+∠EAD=180°,则圆心A到DE的距离等于3.
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知BC=6,∠BAC+∠EAD=180°,则圆心A到DE的距离等于3.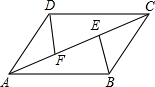 如图,在四边形ABCD中,AD∥BC,AB∥CD且AD=BC,E,F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:△ADF≌△BEC.
如图,在四边形ABCD中,AD∥BC,AB∥CD且AD=BC,E,F为对角线AC上两点,且BE∥DF,请从图中找出一对全等三角形:△ADF≌△BEC. 反比例函数的图象如图所示,则k的值可能0.5.(写出一个即可)
反比例函数的图象如图所示,则k的值可能0.5.(写出一个即可)