题目内容

12．如果关于x的方程x2+4x+k=0（k为常数）有两个不相等的实数根，那么k的范围k＜4．

分析 根据方程有两个不相等的实数根，得到根的判别式的值大于0列出关于k的方程，求出方程的解即可得到k的范围．

解答 解：∵方程x2+4x+k=0有两个不相等的实数根，
∴△=16-4k＞0，
解得：k＜4．
故答案为：k＜4．

点评 此题考查了根的判别式，根的判别式的值大于0时，方程有两个不相等的实数根；根的判别式的值等于0时，方程有两个相等的实数根；根的判别式的值小于0时，方程无解．

练习册系列答案
相关题目
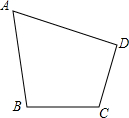2．在四边形ABCD中，∠A=60°，AB⊥BC，AD⊥DC，AB=20cm，CD=10cm，求AD、BC的长．（保留根号）
3．如图，在平行四边形ABCD中，AE⊥BC于点E，3AE=4BE，AB=EC=10，求平行四边形ABCD的面积．
20．若方程（m-1）${x}^{{m}^{2}+1}$+2mx-3=0是关于x的一元二次方程，求m的值．
7．已知x=1是方程x2+bx-2=0的一个根，则b的值是（　　）
A．1B．2C．-2D．-1
17．如图，CD⊥AB于D，GF⊥AB于F，∠1=50°，求∠2度数．
4．已知关于x的方程2（x-1）=3m-1与3x+2=-4的解互为相反数，求m的值．
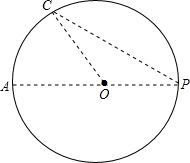1．点P到⊙O上的最大距离为10cm．最小距离为5cm．求⊙O的半径．
解．如图，连PO，直线PO交⊙O于点A、B，设C是⊙O上异于A、B的一点，连OC和PC，则PA=OP+OA=OP=OC＞PC，PB=OB-OP=OC-OP＜PC，∴PA表示点P到⊙O圆周上的最大距离，PB表示点P到⊙O圆周上的最小距离．
设⊙O的半径为R，则$\left\{\begin{array}{l}{R+OP=10}\\{R-OP=5}\end{array}\right.$
解得R=7.5．即⊙O的半径为7.5cm．
你认为以上的解答是否正确．如果不正确？错哪里？请写出正确的解答．
2．若（a+3）2+|b-2|=0，则ab=（　　）
A．9B．-6C．-9D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网