题目内容
3．
如图，在平行四边形ABCD中，AE⊥BC于点E，3AE=4BE，AB=EC=10，求平行四边形ABCD的面积．
分析 根据已知条件设AE=4x，BE=3x，由勾股定理得到AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=5x，求得AE=8，BE=6，根据平行四边形的面积即可得到结论．
解答 解：∵AE⊥BC于点E，3AE=4BE，
∴设AE=4x，BE=3x，
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=5x，
∵AB=EC=10，
∴AE=8，BE=6，
∴BC=16，
∴平行四边形ABCD的面积=AE•BC=8×16=128．
点评 本题考查了平行四边形的性质，平行四边形的面积的计算，勾股定理，熟记平行四边形的面积公式是解题的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
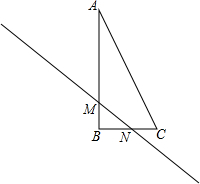如图，在直角三角形ABC中，∠B=90°，点M，N分别在边AB，BC上，且BM=BN，
小彬家的墙上钉着一个用彩绳围成的三角形（如图，单位：cm），小彬通过移动钉子，把它变成一个（如图虚线所示）正三角形，则正三角形的边长为7cm．
小李是一位集邮爱好者，2014年年底，他收藏的邮票数量达到了100枚，到2015年年底达到了200枚，他绘制了一幅如图所示的统计图来表示他的收藏量，合适吗？为什么？
15．已知点P（-2，3），则点P关于原点的对称点的坐标是（ ）
| A． | （3，-2） | B． | （2，-3） | C． | （-3，2） | D． | （-2，-3） |
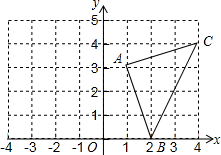如图，A（1，3），B（2，0），C（4，4）．