题目内容

如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°，AC=
6
．求BD的长．
考点：勾股定理
专题：
分析：先根据勾股定理求出AD的长，再由锐角三角函数的定义求出BD的长即可．
解答：解：∵AD⊥BC，垂足为D，∠C=45°，AC=
6
，
∴△ADC是等腰直角三角形，
∴2AD2=AC2，即2AD2=（
6
）2，解得AD=
3
，
∵∠B=60°，
∴BD=
AD
tan60°
=
3
3
=1．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
上周上完体育课，小强从超市买来一瓶结了冰的矿泉水，还未来得及喝，就上课了，于是小强把矿泉水放在了书桌上，其水温与放置时间的关系大致图象为（　　）
A、
B、
C、
D、
（1）化简后再求值：5（3a2b-ab2）-4（-ab2+3a2b），其中a=-1，b=-2．
（2）已知A=y2-ay-1，B=2by2-4y-1，且多项式2A-B的值与字母y的取值无关，求2（a2b-1）-3a2b+2的值．
先化简，再求值：[（2x+y）2-（2x+y）（2x-y）-y（5x+y）]÷
1
2
y，其中x-y=2．
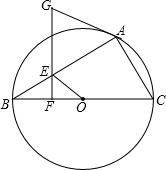如图，已知，⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA=GE．
（1）求证：AG与⊙O相切．
（2）若AC=6，AB=8，BE=3，求线段OE的长．
如图1，抛物线y=x2-2x+k与x轴交于A，B两点，与y轴交于点C（0，-3）．
（1）k=
 
，点A的坐标为
 
，点B的坐标为
 
；
（2）设抛物线的顶点为M，求四边形ABMC的面积；
（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请利用图2，求出点D的坐标；若不存在，说明理由．
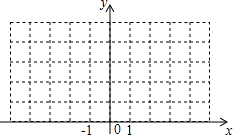如图，在平面直角坐标系中，
（1）描出A（1，5）、B（1，0）、C（4，3）三点．
（2）△ABC的面积是多少？
（3）作出△ABC关于y轴的对称图形．
计算
（1）
(-2)2
+
3-64
+|
3
-2|；
（2）-22+
16
-
3-8
．
在数轴上近似地表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接．4，-1.5，0，-
2
，π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网