题目内容
已知关于x的方程mx=2-x的解为整数,求m的非负整数值.
考点:一元一次方程的解
专题:计算题
分析:方程移项合并,把x系数化为1,表示出解,根据解为整数,确定出m的非负整数值即可.
解答:解:方程变形得:(m+1)x=2,
当m+1≠0,即m≠-1时,解得:x=
,
由x为整数,得到m+1=1或m+1=2,
解得:m=0或m=1,
则m的非负整数值为0和1.
当m+1≠0,即m≠-1时,解得:x=
| 2 |
| m+1 |
由x为整数,得到m+1=1或m+1=2,
解得:m=0或m=1,
则m的非负整数值为0和1.
点评:此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若实数a、b互为相反数,则下列等式中成立的是( )
| A、a-b=0 | B、a+b=0 |
| C、ab=1 | D、ab=-1 |
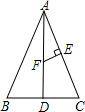 如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.
如图,△ABC中,AB=AC=10,BC=8,AD⊥BC于D,E为AC的中点,EF⊥AC于E,交AD于F,求EF的长度.