题目内容
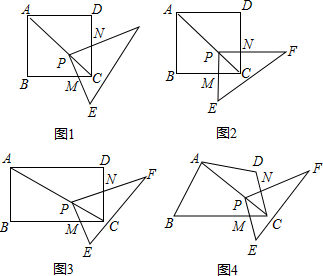
2.如图1,点P在正方形ABCD的对角线AC上,正方形的边长是a,Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N.(1)操作发现:如图2,固定点P,使△PEF绕点P旋转,当PM⊥BC时,四边形PMCN是正方形.填空:①当AP=2PC时,四边形PMCN的边长是$\frac{1}{3}$a;②当AP=nPC时(n是正实数),四边形PMCN的面积是$\frac{{a}^{2}}{(n+1)^{2}}$.
(2)猜想论证
如图3,改变四边形ABCD的形状为矩形,AB=a,BC=b,点P在矩形ABCD的对角线AC上,Rt△PEF的两条直角边PE、PF分别交BC、DC于点M、N,固定点P,使△PEF绕点P旋转,则$\frac{PM}{PN}$=$\frac{a}{b}$.
(3)拓展探究
如图4,当四边形ABCD满足条件:∠B+∠D=180°,∠EPF=∠BAD时,点P在AC上,PE、PF分别交BC,CD于M、N点,固定P点,使△PEF绕点P旋转,请探究$\frac{PM}{PN}$的值,并说明理由.
分析 (1)①先判定△PMC∽△ABC,再根据相似三角形的对应边成比例进行求解;②先用①中的方法求得正方形PMCN的边长,再计算其面积;
(2)先过P作PG⊥BC于G,作PH⊥CD于H,判定△PGM∽△PHN,再根据相似三角形的性质以及平行线分线段成比例定理进行推导计算即可;
(3)先过P作PG∥AB,作PH∥AD,并结合条件∠B+∠D=180°,判定△PGM∽△PHN,再根据相似三角形的性质以及平行线分线段成比例定理进行推导计算即可.
解答 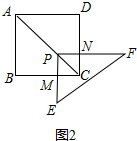 解:(1)①如图2,∵PM⊥BC,AB⊥BC
解:(1)①如图2,∵PM⊥BC,AB⊥BC
∴△PMC∽△ABC
∴$\frac{CP}{CA}$=$\frac{PM}{AB}$
又∵AP=2PC
∴$\frac{PM}{AB}$=$\frac{1}{3}$,即$\frac{PM}{a}$=$\frac{1}{3}$
∴PM=$\frac{1}{3}$a,即正方形PMCN的边长是$\frac{1}{3}$a
②当AP=nPC时(n是正实数),$\frac{PM}{AB}$=$\frac{1}{n+1}$
∴PM=$\frac{1}{n+1}$a
∴四边形PMCN的面积=($\frac{1}{n+1}$a)2=$\frac{{a}^{2}}{(n+1)^{2}}$
(2)如图3,过P作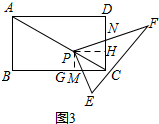 PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°
PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°
∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴$\frac{PM}{PN}$=$\frac{PG}{PH}$
由PG∥AB,PH∥AD可得,$\frac{PG}{AB}=\frac{CP}{CA}=\frac{PH}{AD}$
∵AB=a,BC=b
∴$\frac{PG}{a}=\frac{PH}{b}$,即$\frac{PG}{PH}$=$\frac{a}{b}$
∴$\frac{PM}{PN}$=$\frac{a}{b}$
(3)如图4,过P作PG∥AB,交BC于G,作PH∥AD,交CD于H,则∠HPG=∠DAB
∵∠EPF=∠BAD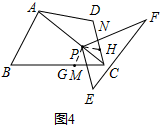
∴∠EPF=∠GPH,即∠EPH+∠HPN=∠EPH+∠GPM
∴∠HPN=∠GPM
∵∠B+∠D=180°
∴∠PGC+∠PHC=180°
又∵∠PHN+∠PHC=180°
∴∠PGC=∠PHN
∴△PGM∽△PHN
∴$\frac{PM}{PN}$=$\frac{PG}{PH}$①
由PG∥AB,PH∥AD可得,$\frac{PG}{AB}$=$\frac{CP}{CA}$=$\frac{PH}{AD}$
即$\frac{PG}{PH}$=$\frac{AB}{AD}$②
∴由①②可得,$\frac{PM}{PN}$=$\frac{AB}{AD}$
点评 本题主要考查了相似三角形的应用以及平行线分线段成比例定理,解决问题的关键是作辅助线构造相似三角形,并根据两角对应相等判定两个三角形相似.解题时注意,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

 全优点练单元计划系列答案
全优点练单元计划系列答案| A. | a•a3=a3 | B. | (ab)3=a3b | C. | a8÷a4=a2 | D. | (a3)2=a6 |
 请从以下两题中任选一题作答,若多选,则按所选的第一题计分.
请从以下两题中任选一题作答,若多选,则按所选的第一题计分.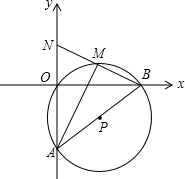 如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.