题目内容
4．已知M（4，2），N（1，2）．（1）若点P在y轴上，且PM+PN最小，求P的坐标；
（2）若点P在x轴上，且PM+PN最小，求P的坐标．
分析 （1）连接MN，延长MN交y轴于P，此时PM+PN最小，根据M、N的坐标即可求得P的坐标．
（2）作点M关于x轴的对称点M′，则M′N交x轴于点P，然后求得直线M′N的函数解析式，继而可得点P的坐标．
解答 解：（1）如图1，连接MN，延长MN交y轴于P，此时PM+PN最小，
∵M（4，2），N（1，2）．
∴P（0，2）；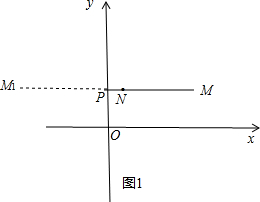
（2）如图2，作点，M关于x轴的对称点M′，则MN′交x轴于点P，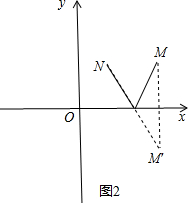
∵M（4，2），
∴M′（4，-2），
设直线M′N的解析式为y=kx+b，$\left\{\begin{array}{l}{4k+b=-2}\\{k+b=2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=\frac{10}{3}}\end{array}\right.$，
∴直线M′N的解析式为y=-$\frac{4}{3}$x+$\frac{10}{3}$，
当y=0时，x=$\frac{5}{2}$，
∴点P的坐标是（$\frac{5}{2}$，0）．
点评 此题考查了最短路径问题和用待定系数法求一次函数解析式；综合运用了一次函数的知识．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
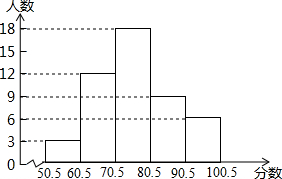某校一次知识竞赛，竞赛成绩（取整数），进行整理后分五组，并绘制成频数分布直方图，结合图形，解答下列问题：
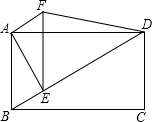如图，四边形ABCD是矩形，E是对角线BD上不同于B，D的任意一点，AF=BE，∠DAF=∠CBD．
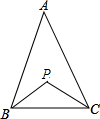如图，在△ABC中，BP、CP分别为∠B、∠C的平分线，请探究∠A和∠P之间存在怎样的数量关系？说说你的理由．
如图，在四边形ABCD中，AB∥CD，AB=4，CD=10，点E，F分别为AC，BD的中点，求EF的长．
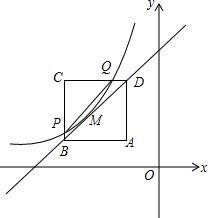如图，正方形ABCD中A（-1，1），B（-3，1），D（-1，3）．反比例函数y=$\frac{k}{x}（x＜0）$的图象经过对角线BD的中点M，与BC、CD的边分别交于点P、Q．