题目内容
12.若一个三位数t=$\overline{abc}$(其中a、b、c不全相等且都不为0),重新排列各数位上的数字必可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为T(t).例如,357的差数T(357)=753-357=396.(1)已知一个三位数$\overline{a1b}$(其中a>b>1)的差数T($\overline{a1b}$)=792,且各数位上的数字之和为一个完全平方数,求这个三位数;
(2)若一个三位数$\overline{ab2}$(其中a、b都不为0)能被4整除,将个位上的数字移到百位得到一个新数$\overline{2ab}$被4除余1,再将新数个位数字移到百位得到另一个新数$\overline{b2a}$被4除余2,则称原数为4的“闺蜜数”.例如:因为612=4×153,261=4×65+1,126=4×31+2,所以612是4的一个闺蜜数.求所有小于500的4的“闺蜜数”t,并求T(t)的最大值.
分析 (1)由一个三位数$\overline{a1b}$(其中a>b>1)的差数T($\overline{a1b}$)=792,可得a=9,再根据三位数$\overline{a1b}$(其中a>b>1)的各数位上的数字之和为一个完全平方数,可得b=16-9-1=6,依此即可求解;
(2)由一个三位数$\overline{ab2}$(其中a、b都不为0)能被4整除,可得b=1或3或5或7或9,再根据将新数个位数字移到百位得到另一个新数$\overline{b2a}$被4除余2并且a<5,可得a=2,从而得到所有小于500的4的“闺蜜数”t,进一步求得T(t)的最大值.
解答 解:(1)∵一个三位数$\overline{a1b}$(其中a>b>1)的差数T($\overline{a1b}$)=792,
∴a=9,
∵三位数$\overline{a1b}$(其中a>b>1)的各数位上的数字之和为一个完全平方数,
∴b=16-9-1=6,
∴这个三位数是916;
(2)∵一个三位数$\overline{ab2}$(其中a、b都不为0)能被4整除,
∴b=1或3或5或7或9,
∵将新数个位数字移到百位得到另一个新数$\overline{b2a}$被4除余2并且a<5,
∴a=2,
∴所有小于500的4的“闺蜜数”t是212,232,252,272,292,
T(t)的最大值是922-229=693.
点评 此题考查了完全平方数,本题主要应用“差数”“闺蜜数”的定义和整数性质,先将三位“差数”进行预选,然后再从中筛选出符合题意的数.这也是解答数学竞赛题的一种常用方法.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
18. 如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
 如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )
如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧$\widehat{OB}$上一点,则∠ACB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 无法确定 |

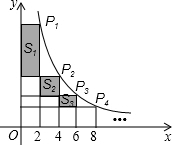 如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)
如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)