题目内容
已知A、B是数轴上两点,A点对应数为12,B点对应数为42.
(1)C是数轴上一点,且AC=2AB,求C点对应的数.
(2)D是数轴上A点左侧一点,动点P从D点出发向右运动,9秒钟到达A点,15秒钟到达B点,求P点运动的速度.
(3)在(2)的条件下,又有2个动点Q和R分别从A、B和P点同时向右运动,Q的速度为每秒一个单位,R的速度为每秒两个单位,求经过几秒,P和Q的距离等于Q和R的距离的3倍.
(1)C是数轴上一点,且AC=2AB,求C点对应的数.
(2)D是数轴上A点左侧一点,动点P从D点出发向右运动,9秒钟到达A点,15秒钟到达B点,求P点运动的速度.
(3)在(2)的条件下,又有2个动点Q和R分别从A、B和P点同时向右运动,Q的速度为每秒一个单位,R的速度为每秒两个单位,求经过几秒,P和Q的距离等于Q和R的距离的3倍.
考点:一元一次方程的应用,数轴
专题:
分析:(1)可求得AB=30,所以AC=60,设C点对应的数为x,则有AC=|x-12|=60,可求得x;
(2)设运动速度为每秒y个单位长度,则有(15-9)y=30,可求得y的值;
(3)设经过z秒,则5z-45-z=3(30+2z-t),可求得z的值.
(2)设运动速度为每秒y个单位长度,则有(15-9)y=30,可求得y的值;
(3)设经过z秒,则5z-45-z=3(30+2z-t),可求得z的值.
解答:解:(1)由题意可知AB=42-12=30,所以AC=2AB=60,
设点C对应的数为x,
则有AC=|x-12|,所以有|x-12|=60,
解得x=72或-48,
即点C对应的数为72或-48;
(2)设P点运动速度为每秒y个单位,
由题意可得方程(15-9)y=30,
解得y=5,
即P点每秒运动5个单位;
(3)由(2)知P点每秒运动5个单位,且Q为每秒1个单位,R为每秒2个单位,
设经过z秒,P和Q的距离等于Q和R的距离的3倍,
根据题意可列方程:|5t-45-t|=3(30+2t-t),解得t=135或-
(舍去),
即经过135秒,P和Q的距离等于Q和R的距离的3倍.
设点C对应的数为x,
则有AC=|x-12|,所以有|x-12|=60,
解得x=72或-48,
即点C对应的数为72或-48;
(2)设P点运动速度为每秒y个单位,
由题意可得方程(15-9)y=30,
解得y=5,
即P点每秒运动5个单位;
(3)由(2)知P点每秒运动5个单位,且Q为每秒1个单位,R为每秒2个单位,
设经过z秒,P和Q的距离等于Q和R的距离的3倍,
根据题意可列方程:|5t-45-t|=3(30+2t-t),解得t=135或-
| 25 |
| 7 |
即经过135秒,P和Q的距离等于Q和R的距离的3倍.
点评:本题主要考查一元一次方程的应用,解题的关键是由已知条件找到题目中的等量关系,列出方程.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 如图所示是某家庭去年开支的扇形统计图,根据统计图,回答下列问题:
如图所示是某家庭去年开支的扇形统计图,根据统计图,回答下列问题: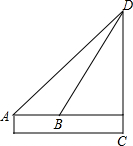 小明想测量CD的高度,他在A处仰望塔顶,仰角为45°,再往塔的方向前进50m至B处,测得仰角为60°,小明身高为1.5m,那么该塔有多高?
小明想测量CD的高度,他在A处仰望塔顶,仰角为45°,再往塔的方向前进50m至B处,测得仰角为60°,小明身高为1.5m,那么该塔有多高?