题目内容
7.一元二次方程x2-4x+1=0配方后可变形为( )| A. | (x-2)2=5 | B. | (x+2)2=5 | C. | (x-2)2=3 | D. | (x+2)2=3 |
分析 方程常数项移到右边,两边加上4变形即可得到结果.
解答 解:方程变形得:x2-4x=-1,
配方得:x2-4x+4=3,即(x-2)2=3.
故选:C.
点评 此题考查了解一元二次方程-配方法,熟练掌握解方程的步骤与方法是解决问题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
17.某商店一套服装进价为300元,如果按标价的八折销售可获利80元,那么该服装的标价是( )
| A. | 375元 | B. | 380元 | C. | 450元 | D. | 475元 |
18. 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
 如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )
如图,在边长为9cm的等边三角形ABC中,D为BC上一点,且BD=3cm,E在AC上,∠ADE=60°,则AE的长为( )| A. | 2cm | B. | 5cm | C. | 6cm | D. | 7cm |
2.下列长度的三条线段能组成直角三角形的是( )
| A. | 4,5,6 | B. | 2,3,4 | C. | 1,1,$\sqrt{2}$ | D. | 1,2,2 |
17.元旦期间,某玩具店从玩具批发市场批发玩具进行零售,部分玩具批发价格与零售价格如下表:
请解答下列问题:
(1)第一天,该玩具店批发A,B两种型号玩具共59个,用去了1344元钱,这两种型号玩具当天全部售完后一共能赚多少元钱?
(2)第二天,该玩具店用第一天全部售完后的总零售价钱批发A,B,C三种型号玩具中的两种玩具共68个,且当天全部售完,请通过计算说明该玩具店第二天应如何进货才能使全部售完后赚的钱最多?
| 玩具型号 | A | B | C |
| 批发价(元/个) | 20 | 24 | 28 |
| 零售价(元/个) | 25 | 30 | 40 |
(1)第一天,该玩具店批发A,B两种型号玩具共59个,用去了1344元钱,这两种型号玩具当天全部售完后一共能赚多少元钱?
(2)第二天,该玩具店用第一天全部售完后的总零售价钱批发A,B,C三种型号玩具中的两种玩具共68个,且当天全部售完,请通过计算说明该玩具店第二天应如何进货才能使全部售完后赚的钱最多?
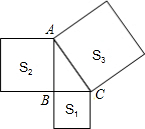 如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S1、S2、S3,若S2=4,S3=6,则S1=( )
如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S1、S2、S3,若S2=4,S3=6,则S1=( )
