题目内容
如图3－83所示，等腰三角形ABC内接于半径为5的⊙O中，AB＝AC，且tan B＝
．
(1)求BC的长；
(2)求AB边上的高．
解：(1)连接OA交BC于D，连接OB，OC，则AO垂直平分线段BC．设AD＝x，∵tan B＝，∴BD＝3x．在Rt△ODB中，(5－x)2＋(3x)2＝52，解得x＝1，∴BC＝2BD＝6． (2)过C作CE⊥AB交BA的延长线于E，∵tan B＝，BC＝
6，∴CE2＋(3CE)2＝62，∴CE＝
．
练习册系列答案
智能训练练测考系列答案
相关题目
的半径为4cm,点
到圆心
的距离为3cm，则点如图，当半径分别是5和r的两圆⊙O1和⊙O2外切时，它们的圆心距O1O2=8，则⊙O2的半径r为（ ）
|
| A． | 12 | B． | 8 | C． | 5 | D． | 3 |
半圆O相切时（如图①），求∠ODC的度数；
)
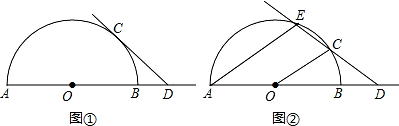
D．y＝－