题目内容
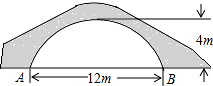
已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
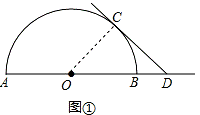
(1)当直线CD与 半圆O相切时(如图①),求∠ODC的度数;
半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如 图②),设另一交点为E,连接AE,若AE∥OC,
图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系? 为什么?
为什么?
②求∠ODC的度数.
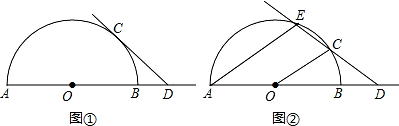
解:(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45° ;
;
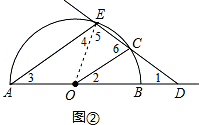
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°﹣2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
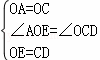
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5 +∠6=180°,即:x+2x+2x=180°,
+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 .其中正确的有( )
.其中正确的有( ) 直径的半圆分别交AC,BC于D,E,O为圆心,求∠DOE的度数.
直径的半圆分别交AC,BC于D,E,O为圆心,求∠DOE的度数.
 .
.

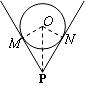 = 60°,则
= 60°,则 OP =( )
OP =( )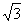 cm
cm 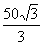 cm D.50
cm D.50
 cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
cm,底面半径r=2cm,则圆锥体的全面积为( )cm2.
 π B 8π C 12π D (4
π B 8π C 12π D (4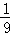 (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .