题目内容
18.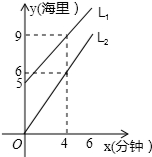 L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象如图.
L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象如图.(1)计算走私船与公安快艇的速度分别是多少?
(2)公安快艇能否追上走私船?若能,那么几分钟追上?若不能,说明理由.
分析 (1)先设出l1、l2的函数表达式,再用待定系数法进行求解,即可得出答案;
(2)公安快艇追上走私船时令y1=y2,再进行求解即可.
解答 解:(1)设l1的函数表达式是y1=k1x+b,
l2的函数表达式是y2=k2x,
由图象可知,l1过点(0,5)、(4,9),
$\left\{\begin{array}{l}{9={4k}_{1}+b}\\{b=5}\end{array}\right.$,
解得k1=1,
l1的函数表达式是y1=x+5,
由图象可知,l2过点(4,6),
6=4k2,
解得:k2=$\frac{3}{2}$,
l2的函数表达式是y2=$\frac{3}{2}$x.
(2)根据题意得:
x+5=$\frac{3}{2}$x,
解得x=10.
答:公安快艇10分钟能追上走私船.
点评 本题考查了一次函数的应用,同时也考查了识别函数图象的能力,观察图象提供的信息,再分析求解是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列图中是四棱柱的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
8.某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下(单位:千米):
(1)求收工时检修小组距离A地多远?
(2)第几次纪录时检修小组距离A地最远?
(3)若每千米耗油0.5升,每升汽油需6元,问检修小组工作一天需汽油费多少元?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +8 | -9 | +10 | +4 | -6 | -2 |
(2)第几次纪录时检修小组距离A地最远?
(3)若每千米耗油0.5升,每升汽油需6元,问检修小组工作一天需汽油费多少元?
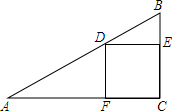 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. 如图,截面依次是长方形、三角形、圆形.
如图,截面依次是长方形、三角形、圆形.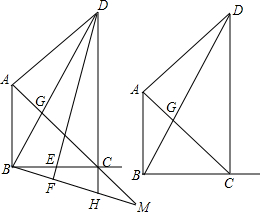
 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.
如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.