题目内容
如图，梯形ABCD两腰DA，CB的延长线交于O．已知S△AOB=4，S△AOC=9，则S梯形ABCD=
- A.25
- B.16.25
- C.16
- D.15.25
B
分析：由于△AOB与△AOC是等高的三角形，求出OB：OC=4：9，由平行线得出△OAB∽△ODC，求出△ODC的面积，相减即可得出答案．
解答：∵S△AOB=4，S△AOC=9，△AOB边OB上的高和△AOC的边OC上的高相等，
∴
=
=
，
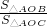∵AB∥DC，
∴△OAB∽△ODC，
∴
=
=
，
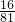∴S△ODC=
，
S梯形ABCD=S△ODC-S△ODC=-4=16.25．
故选B．
点评：本题主要考查了等高三角形的面积比与边长的比例关系，能够建立等式并熟练求解．
分析：由于△AOB与△AOC是等高的三角形，求出OB：OC=4：9，由平行线得出△OAB∽△ODC，求出△ODC的面积，相减即可得出答案．
解答：∵S△AOB=4，S△AOC=9，△AOB边OB上的高和△AOC的边OC上的高相等，
∴
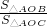==，∵AB∥DC，
∴△OAB∽△ODC，
∴
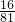==，∴S△ODC=
，S梯形ABCD=S△ODC-S△ODC=
-4=16.25．故选B．
点评：本题主要考查了等高三角形的面积比与边长的比例关系，能够建立等式并熟练求解．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
如图，梯形ABCD两腰DA，CB的延长线交于O．已知S△AOB=4，S△AOC=9，则S梯形ABCD=（ ）| A、25 | B、16.25 | C、16 | D、15.25 |
如图，梯形ABCD两条对角线交于E，CD上取一点F，使得EF∥BC，若AD=1，BC=2，则
= ．
