题目内容
18.为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):(1)报名参加课外活动小组的学生共有100人,将条形图补充完整;
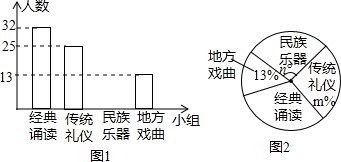
(2)扇形图中m=25,n=108;
(3)根据报名情况,学校决定从报名“经典诵读”小组的甲、乙、丙、丁四人中随机安排两人到“地方戏曲”小组,甲、乙恰好都被安排到“地方戏曲”小组的概率是多少?请用列表或画树状图的方法说明.
分析 (1)用地方戏曲的人数除以其所占的百分比即可求得总人数,减去其它小组的频数即可求得民族乐器的人数,从而补全统计图;
(2)根据各小组的频数和总数分别求得m和n的值即可;
(3)列树状图将所有等可能的结果列举出来,然后利用概率公式求解即可.
解答 解:(1)∵根据两种统计图知地方戏曲的有13人,占13%,
∴报名参加课外活动小组的学生共有13÷13%=100人,
参加民族乐器的有100-32-25-13=30人,
统计图为:
(2)∵m%=$\frac{25}{100}$×100%=25%,
∴m=25,
n=$\frac{30}{100}$×360=108,
故答案为:25,108;
(3)树状图分析如下:
∵共有12种情况,恰好选中甲、乙的有2种,
∴P(选中甲、乙)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了扇形统计图、条形统计图及列表与树状图法求概率的知识,解题的关键是能够列树状图将所有等可能的结果列举出来,难度不大.

练习册系列答案
相关题目
9.设x1,x2是一元二次方程x2-2x-3=0的两根,则x12+x22=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
6.下列说法正确的是( )
| A. | “购买1张彩票就中奖”是不可能事件 | |
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
3.下列命题中,是假命题的是( )
| A. | 对顶角相等 | |
| B. | 同旁内角互补 | |
| C. | 两点确定一条直线 | |
| D. | 角平分线上的点到这个角的两边的距离相等 |
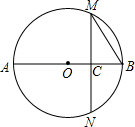 如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为$\frac{1}{2}$.
如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为$\frac{1}{2}$. 如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是24cm3.
如图是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是24cm3.