题目内容
8. 如图,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么cos∠ABD的值是$\frac{1}{3}$.
如图,已知AB是⊙O的直径,弦CD⊥AB,AC=2$\sqrt{2}$,BC=1,那么cos∠ABD的值是$\frac{1}{3}$.
分析 由圆周角定理得出∠ACB=90°,∠ABD=∠ABC,由勾股定理求出AB,因而求sin∠ABD的值的问题,就可以转化为求∠ABC的三角函数的值的问题.
解答 解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=3,
∵CD⊥AB,
∴$\widehat{AD}=\widehat{AC}$,
∴∠ABD=∠ABC,
∴cos∠ABD=cos∠ABC=$\frac{BC}{AB}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了圆周角定理、勾股定理、垂径定理和锐角三角函数的定义;熟练掌握垂径定理,由圆周角定理得出∠ABD=∠ABC是解决问题的关键.

练习册系列答案
相关题目
19.在一个不透明的布袋中,红色、黑色的球共有10个,它们除颜色外其他完全相同.张宏通过多次摸球试验后发现其中摸到红球的频率稳定在20%附近,则口袋中红球的个数很可能是( )
| A. | 2个 | B. | 5个 | C. | 8个 | D. | 10个 |
13.下列四幅图中,∠1和∠2是同位角的是( )


| A. | ① | B. | ①② | C. | ①②③ | D. | ①③④ |
17. 如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
 如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是( )| A. | 伟 | B. | 大 | C. | 的 | D. | 国 |
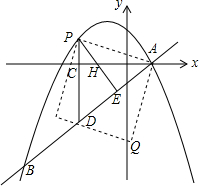 如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$.
如图,在平面直角坐标系中,直线y=kx+n(k≠0)与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点,点A在x轴上,OA=2,点B的横坐标为-8,且tan∠OAB=$\frac{3}{4}$.