题目内容
12.由下列条件不能判定△ABC为直角三角形的是( )| A. | (b+c)(b-c)=a2 | B. | a=3+k,b=4+k,c=5+k(k>0) | ||
| C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=1:3:2 |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可.
解答 解:A、∵(b+c)(b-c)=a2,∴b2-c2=a2,即a2+c2=b2,故是直角三角形,正确
B、∵(3+k)2+(4+k)2≠(5+k)2,故不能判定是直角三角形
C、∵∠A+∠B=∠C,∴∠C=90°,故是直角三角形,正确;
D、∵∠A:∠B:∠C=1:3:2,∴∠B=$\frac{3}{6}$×180°=90°,故是直角三角形,正确;
故选B.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
2.①平行四边形,②矩形,③菱形,④正方形中,对角线的交点到各边中点的距离都相等的是( )
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
3.下面的多项式中,能因式分解的是( )
| A. | m2-2m+1 | B. | m2+n | C. | m2-m+1 | D. | m2-n |
 (1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;
(1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;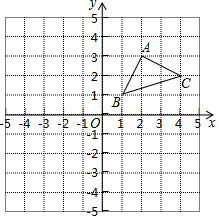 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2). 如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1). 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.