题目内容
17.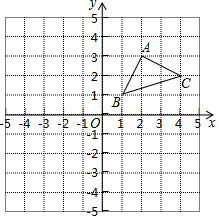 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).(1)连接A、B、C三点,请在如图中作出△ABC关于x轴对称的图形△A′B′C′并直接写出各对称点的坐标.
(2)求△ABC的面积.
(3)若M(x,y)是△ABC内部任意一点,请直接写出点M在△A′B′C′内部的对应点M1的坐标.
分析 (1)直接利用关于x轴对称点的性质得出对应点位置进而得出答案;
(2)利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(3)利用关于x轴对称点的性质得出答案.
解答  解:(1)如图所示:△A′B′C′即为所求,A′(2,-3),B′(1,-1),C′(4,-2);
解:(1)如图所示:△A′B′C′即为所求,A′(2,-3),B′(1,-1),C′(4,-2);
(2)△ABC的面积为:2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=2.5;
(3)若M(x,y)是△ABC内部任意一点,则点M在△A′B′C′内部的对应点M1的坐标为:(x,-y).
点评 此题主要考查了轴对称变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
8.下列函数中,y随x的增大而减小的函数是( )
| A. | y=-2x+8 | B. | y=3x+5 | C. | y=4x-3 | D. | y=6x |
5.描述一个圆形平移或旋转后正确的说法是( )
| A. | 图形形状与位置都不变 | B. | 图形形状与大小都不变 | ||
| C. | 图形形状与大小都变 | D. | 图形形状与位置都变 |
12.由下列条件不能判定△ABC为直角三角形的是( )
| A. | (b+c)(b-c)=a2 | B. | a=3+k,b=4+k,c=5+k(k>0) | ||
| C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=1:3:2 |
2.不等式2x-3≤1的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
9.下面说法正确的是( )
| A. | 检测小食品质量应采用全面调查 | |
| B. | 从2万名考生中抽取100名考生作为样本,样本容量是2万 | |
| C. | 反映你本学年数学成绩的变化情况宜采用扇形统计图 | |
| D. | 一组数据有80分,最大值是141,最小值是60,取组距为10,可分为9组 |
 (b为常数)的图象位于
(b为常数)的图象位于 轴下方的部分沿
轴下方的部分沿 轴翻折至其上方后,所得的折线是函数
轴翻折至其上方后,所得的折线是函数 (b为常数)的图象.若该图象在直线y=2下方的点的横坐标
(b为常数)的图象.若该图象在直线y=2下方的点的横坐标 满足
满足 ,则b的取值范围为____.
,则b的取值范围为____.