题目内容
19.若x1、x2是关于x一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=$-\frac{b}{a}$,x${\;}_{1}{x}_{2}=\frac{c}{a}$,把它们称为一元二次方程根与系数关系定理.已知x1、x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两个实数根.(1)若(x1-1)(x2-1)=28,求m的值.
(2)已知等腰△ABC的一腰长为7,若x1、x2恰好是△ABC另外两边的边长,求这个三角形的周长.
分析 (1)根据韦达定理得x1+x2、x1x2,再代入到(x1-1)(x2-1)=28即x1x2-(x1+x2)+1=28中解方程可得m的值,两个值根据方程有解考虑取舍;
(2)将x=7代入方程求出m的值,将m的两个值分别代回原方程,分别解每一个方程求出x的值,根据三角形三边关系取舍,最后三边相加可得周长.
解答 解:(1)∵x1、x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两个实数根,
∴x1+x2=2(m+1),x1x2=m2+5,
∵(x1-1)(x2-1)=28,即x1x2-(x1+x2)+1=28,
∴m2+5-2(m+1)+1=28,解得:m=-4或m=6,
当m=-4时原方程无解,
∴m=6;
(2)当等腰三角形的腰长为7时,即方程的一个解为7,
将x=7代入原方程得:49-14(m+1)+m2+5=0,
解得:m=10或m=4,
当m=10时,方程为x2-22x+105=0,解得:x=7或x=15,
∵7+7<15,不能组成三角形;
当m=4时,方程为x2-10x+21=0,解得:x=3或x=7,
此时三角形的周长为:7+7+3=17.
点评 本题主要考查一元二次方程根与系数的关系、解方程、等腰三角形性质等知识点,根据韦达定理得到此方程的两根和与两根积是解题的根本,熟悉方程的解及三角形三边关系是第2题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
7. 如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
 如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 三视图 |
4.将抛物线y=x2先向右平移2个单位长度,再向上平移4个单位长度,得到的新的抛物线的解析式为( )
| A. | y=(x+2)2+4 | B. | y=(x+2)2-4 | C. | y=(x-2)2+4 | D. | y=(x-2)2-4 |
9.抛三枚硬币,两个正面和一个反面朝上的概率是( )
| A. | $\frac{7}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{8}$ |
 在平面直角坐标系中有一个正方形OACB,点A坐标为(4,0),M、N分别是OA、AC上的两个动点,当M点在OA上运动时,一直保持BM和MN垂直.
在平面直角坐标系中有一个正方形OACB,点A坐标为(4,0),M、N分别是OA、AC上的两个动点,当M点在OA上运动时,一直保持BM和MN垂直.
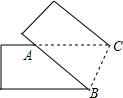 将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.