题目内容
2. 如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2$\sqrt{2}$,则∠BOC=30°或150°°.
如图,在半径为2的⊙O中,弦AB=2,⊙O上存在点C,使得弦AC=2$\sqrt{2}$,则∠BOC=30°或150°°.
分析 作OD⊥AB于D,OE⊥AC于E,连结OA,根据垂径定理得AD=$\frac{1}{2}$AB=1,AE=$\sqrt{2}$,再根据勾股定理可计算出OE,OD,根据角的和差得到得到∠BAC,然后根据圆周角定理求解.
解答 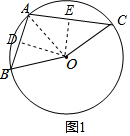 解:如图1,作OD⊥AB于D,OE⊥AC于E,连结OA,OA=2,如图,
解:如图1,作OD⊥AB于D,OE⊥AC于E,连结OA,OA=2,如图,
∴AD=BD=$\frac{1}{2}$AB=1,AE=CE=$\frac{1}{2}$AC=$\sqrt{2}$,
在Rt△OAE中,OE=$\sqrt{2}$,
∴∠EAO=45°,
在Rt△OAD中,OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=$\sqrt{3}$,
∴∠DAO=60°,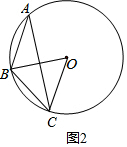
∴∠BAC=45°+60°=105°,
∴∠BOC=150°,
如图2,同理:∠BAC=60°-45°=15°,
∴∠BOC=30°,
故答案为150°或30°.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和解直角三角形.

练习册系列答案
相关题目
12.已知长方形ABCD,一条直线将该长方形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N的度数和不可能为( )
| A. | 360° | B. | 540° | C. | 720° | D. | 630° |
13.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
| A. | 316×106 | B. | 31.6×107 | C. | 3.16×108 | D. | 0.316×109 |
20.4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | ±16 | D. | 16 |
1. 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
 直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )| A. | 30° | B. | 36° | C. | 45° | D. | 72° |
 如图1,将边长为a的大正方形剪去一个边长为b的小正方形并沿图中的虚线剪开,拼接后得到图2,这种变化可以用含字母a,b的等式表示为a2-b2=(a+b)(a-b).
如图1,将边长为a的大正方形剪去一个边长为b的小正方形并沿图中的虚线剪开,拼接后得到图2,这种变化可以用含字母a,b的等式表示为a2-b2=(a+b)(a-b). 如图,在边长为1的小正方形构成的网格中,有一个半径为1的⊙O,且圆心在格点上,tan∠AED的值为$\frac{1}{2}$.
如图,在边长为1的小正方形构成的网格中,有一个半径为1的⊙O,且圆心在格点上,tan∠AED的值为$\frac{1}{2}$.