题目内容
3.已知AB∥CD,分别探讨下面的三个图形中,∠APC与∠A、∠C之间的关系,并请你从所得的三个关系中任选一个,说明成立的理由.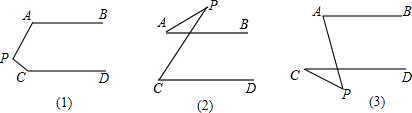
分析 图(1),首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
图(2),由AB∥CD,根据两直线平行,同位角相等,即可求得∠1=∠C,又由三角形外角的性质,即可求得答案;
图(3),由AB∥CD,根据两直线平行,同位角相等,即可得∠1=∠A,然后由三角形外角的性质,即可求得∠A=∠C+∠APC;
解答 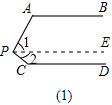 解:如图(1):∠APC=∠A+∠C,
解:如图(1):∠APC=∠A+∠C,
如图(2):∠C=∠A+∠APC;
如图(3):∠A=∠C+∠APC.
如图(1):∠APC=∠A+∠C,
过点P作PE∥AB,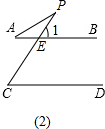
∵AB∥CD,
∴AB∥CD∥PE,
∴∠1=∠A,∠2=∠C,
∴∠APC=∠1+∠2=∠A+∠C;
图(2):∠C=∠APC+∠A,
∵AB∥CD,
∴∠1=∠C,
∵∠1=∠A+∠APC,
∴∠C=∠A+∠APC.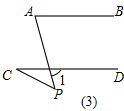
图(3),∵AB∥CD,
∴∠1=∠A,
∵∠1=∠C+∠APC,
∴∠A=∠C+∠APC.
点评 此题考查了平行线的性质与三角形外角的性质.此题难度不大,解题的关键是注意掌握两直线平行,同位角相等;两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意辅助线的作法.

练习册系列答案
相关题目
13.已知直线y=$\frac{-(n+1)}{n+2}$x+$\frac{1}{n+2}$(n为正整数)与坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2012的值为( )
| A. | $\frac{503}{2015}$ | B. | $\frac{1006}{2015}$ | C. | $\frac{1006}{2014}$ | D. | $\frac{503}{2014}$ |
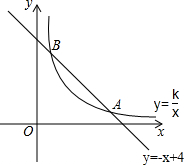 如图,函数y=-x+4的图象与函数$y=\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.
如图,函数y=-x+4的图象与函数$y=\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.