Question

9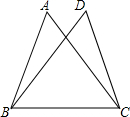．如图，△ABC≌△DCB，那么，
相等的边是：AB与DC，AC与DB，BC与CB；
相等的角是：∠A与∠D，∠ABC与∠DCB，∠ACB与∠DBC．

Answer 1

分析 直接根据全等三角形的性质进行判断．

解答 解：∵△ABC≌△DCB，
∴AB=DC，AC=DB，BC=CB，∠A=∠D，∠ABC=∠DCB，∠ACB=∠DBC，
即AB与DC，AC与DB，BC与CB是对应边；∠A与∠D，∠ABC与∠DCB，∠ACB与∠DBC是对应角．
故答案为AB与DC，AC与DB，BC与CB；∠A与∠D，∠ABC与∠DCB，∠ACB与∠DBC．

点评 本题考查了全等三角形的性质：全等三角形的性质是证明线段和角相等的理论依据，应用时要会找对应角和对应边．