题目内容
1.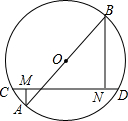 如图,AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.
如图,AB为⊙O的直径,CD为弦,AM⊥CD于M,BN⊥CD于N.(1)求证:CM=DN.
(2)若AB=10,CD=8,求BN-AM的值.
分析 (1)过O作OF⊥CD于F,利用平行线等分线段定理得到MF=NF,利用垂径定理得到:CF=NF,即可得到结论;(2)设AB与CD相交于E,利用垂径定理可以算出OF=3,设OE=x,则EB=x+5,AE=5-x,利用△EBN∽△EOF得到BN:3=(5+x):x,利用△AME∽△OFE得到AM:3=(5-x):x,两式相减即可得到:(BN-AM):3=2,从而得到答案.
解答  解:(1)过O作OF⊥CD于F,
解:(1)过O作OF⊥CD于F,
∵AM⊥CD于M,BN⊥CD于N,
∴AM∥FO∥NB.
∵OA=OB,由平行线等分线段定理得:MF=NF,
∵OF⊥CD,O为圆心,
∴CF=FD,
∴MC=ND;
(2)连结OD,
∵AB=10,CD=8,
∴OD=5,FD=4,
∴OF=3,
OE=x,则EB=x+5,AE=5-x,
∵NB∥FO,
∴△EBN∽△EOF,
∴BN:3=(5+x):x,①
∵MA∥FO,△AME∽△OFE,
∴AM:3=(5-x):x,②
两式相减即可得到:(BN-AM):3=2,
∴BN-AM=6.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
4.若二次三项式4x2-(m-3)x+1是一个完全平方式,则m的值为( )
| A. | 7 | B. | -1 | C. | 4或-4 | D. | 7或-1 |
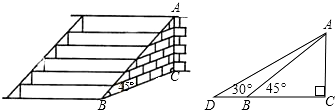
12. 如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
 如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )| A. | 5 | B. | 13 | C. | 17 | D. | 19 |
16. 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.下列计算结果错误的是( )
| A. | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B. | |-$\sqrt{2}$|=$\sqrt{2}$ | C. | $\sqrt{12}÷\sqrt{3}=2$ | D. | $\sqrt{2}÷\sqrt{3}=\sqrt{5}$ |
10.下列说法错误的是( )
| A. | 角内到角两边距离相等的点在角平分线上 | |
| B. | 角平分线上的点到角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三边的距离相等 | |
| D. | 到三角形三边距离相等的点是三条角平分线的交点 |