Question

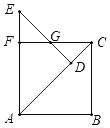
【题目】如图，在△ABC中，∠B＝90°，AB＝BC＝4，把△ABC绕点A逆时针旋转45°得到△ADE，过点C作CF⊥AE于F，DE交CF于G，则四边形ADGF的周长是（　　）

A.8B.4+4C.8+D.8

Answer 1

【答案】D

【解析】

如图，连接AG，由旋转的性质和等腰直角三角形的性质可得AD=AB=4，∠EAD=∠CAB=45°，可求∠FAB=90°，CD=AC-AD=4-4，可证四边形ABCF是正方形，AF=CF=AB=4=AD，∠AFC=∠FCB=90°，由“HL”可证Rt△AGF≌Rt△AGD，可得FG=GD=4-4，即可求解．

如图，连接AG，

∵∠B＝90°，AB＝BC＝4，

∴∠CAB＝∠ACB＝45°，AC＝4，

∵把△ABC绕点A逆时针旋转45°得到△ADE，

∴AD＝AB＝4，∠EAD＝∠CAB＝45°，

∴∠FAB＝90°，CD＝AC﹣AD＝4﹣4，

∵∠B＝90°＝∠FAB，CF⊥AE，

∴四边形ABCF是矩形，且AB＝BC＝4，

∴四边形ABCF是正方形，

∴AF＝CF＝AB＝4＝AD，∠AFC＝∠FCB＝90°，

∴∠GCD＝45°，且∠GDC＝90°，

∴∠GCD＝∠CGD＝45°，

∴CD＝GD＝4﹣4，

∵AF＝AD，AG＝AG，

∴Rt△AGF≌Rt△AGD（HL）

∴FG＝GD＝4﹣4，

∴四边形ADGF的周长＝AF+AD+FG+GD＝4+4+4﹣4+4﹣4＝8，

故选：D．